Conducting cable surrounded by two cylindrical shells

[lorenz0]

Homework Statement

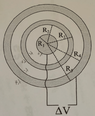
Consider a long conducting cylinder, of radius $R_1$. It is surrounded by two conducting cylindrical shells, the first one with internal radius $R_2$ and external radius $R_3$ and the second one with internal radius $R_4$ and external radius $R_5$. If we put a charge density $+\lambda$ on the conducting inner cylinder of radius $R_1$ the first shell at $R_2$ gets a charge density $-\lambda$, at $R_3$ it gets $+\lambda$ and the second shell at $R_4$ gets a charge density $-\lambda$ at $R_4$ and $+\lambda$ at $R_5$.
(a) Knowing that the inner cylinder and the outermost shell are mantained at a known potential difference $\Delta V$, find out the value of $\lambda$ (assuming the various radii are known.)

(b) Now the outermost shell is connected to the ground. What is the value of $V(r>-R_5)-V(r_{middle})$ where $R_2<r_{middle}<R_3$?

Relevant Equations

$V_A-V_B=-\int_{A}^{B}\vec{E}\cdot d\vec{l}$, $\vec{E}=\frac{\lambda}{\varepsilon_0}\hat{n}$

What I have done:

(a) If we start at $R_5$ then we have $\Delta V=-\int_{R_5}^{R_1}\vec{E}\cdot d\vec{l}=-(\int_{R_5}^{R_4}\vec{0}\cdot d\vec{l}+\int_{R_4}^{R_3}\frac{\lambda}{\varepsilon_0}dl+\int_{R_3}^{R_2}\vec{0}\cdot d\vec{l}+\int_{R_2}^{R_1}\frac{\lambda}{\varepsilon_0}dl=-\lambda( \frac{\lambda}{\varepsilon_0}(R_3-R_4) +\frac{\lambda}{\varepsilon_0}(R_1-R_2))=\frac{\lambda}{\varepsilon_0}(R_4-R_3+R_2-R_1).$

(b) $V(r>R_5)-V(r_{middle})=-\int_{r}^{r_{m}}\vec{E}\cdot d\vec{l}=-(\int_{R_5}^{R_4}\frac{\lambda}{\varepsilon_0}dl+\int_{R_3}^{r_m}\frac{\lambda}{\varepsilon_0}dl)=-\left( \frac{\lambda}{\varepsilon_0}(R_4-R_5)+\frac{\lambda}{\varepsilon_0}(r_m-R_3)\right)=\frac{\lambda}{\varepsilon_0}\left(R_5-R_4+R_3-r_{middle}\right)$.

Is this correct? I would be grateful for some feedback regarding my solution and also for advice about how to tackle these kind of problems with nested conducting shells. Thanks.

 

[kuruman]

Your method of doing a line integral is generally correct. It's the implementation that troubles me. Most importantly, where did you get that the electric is $\vec{E}=\frac{\lambda}{\varepsilon_0}\hat{n}$? My first recommendation for tackling problems of this kind is to use Gauss's law to find the field in all regions of interest. Do that and start over.

 

[lorenz0]

Your method of doing a line integral is generally correct. It's the implementation that troubles me. Most importantly, where did you get that the electric is $\vec{E}=\frac{\lambda}{\varepsilon_0}\hat{n}$? My first recommendation for tackling problems of this kind is to use Gauss's law to find the field in all regions of interest. Do that and start over.

Thanks for your reply. Following your advice, by considering each time a coaxial cylindrical surface, I get that $\vec{E}=\begin{cases}\frac{\lambda R_1}{\varepsilon_0 r}\hat{n} & R_1 <r<R_2\\ \frac{\lambda R_3}{\varepsilon_0 r}\hat{n} & R_3<r<R_4\\ \frac{\lambda R_5}{\varepsilon_0 r}\hat{n} & r>R_5\\ \end{cases}$ so for part (a): $\Delta V=-\left( \int_{R_4}^{R_3}\frac{\lambda R_3}{\varepsilon_0 r} dr +\int_{R_2}^{R_1}\frac{\lambda R_1}{\varepsilon_0 r} dr \right)=\frac{\lambda}{\varepsilon_0}\left( R_3\ln(\frac{R_4}{R_3})+R_1\ln(\frac{R_2}{R_1})) \right)$ and for part (b): $V(r>R_5)-V(r_{middle})=-\left( \int_{R_4}^{R_3}\frac{\lambda R_3}{\varepsilon_0 r}dr+\int_{R_3}^{r_m}0 dr\right)=\frac{\lambda R_3}{\varepsilon_0}\ln(\frac{R_4}{R_3}).$
Is my reasoning correct? Thanks.

 

[kuruman]

Thanks for your reply. Following your advice, by considering each time a coaxial cylindrical surface, I get that $\vec{E}=\begin{cases}\frac{\lambda R_1}{\varepsilon_0 r}\hat{n} & R_1 <r<R_2\\ \frac{\lambda R_3}{\varepsilon_0 r}\hat{n} & R_3<r<R_4\\ \frac{\lambda R_5}{\varepsilon_0 r}\hat{n} & r>R_5\\ \end{cases}$ so for part (a): $\Delta V=-\left( \int_{R_4}^{R_3}\frac{\lambda R_3}{\varepsilon_0 r} dr +\int_{R_2}^{R_1}\frac{\lambda R_1}{\varepsilon_0 r} dr \right)=\frac{\lambda}{\varepsilon_0}\left( R_3\ln(\frac{R_4}{R_3})+R_1\ln(\frac{R_2}{R_1})) \right)$ and for part (b): $V(r>R_5)-V(r_{middle})=-\left( \int_{R_4}^{R_3}\frac{\lambda R_3}{\varepsilon_0 r}dr+\int_{R_3}^{r_m}0 dr\right)=\frac{\lambda R_3}{\varepsilon_0}\ln(\frac{R_4}{R_3}).$
Is my reasoning correct? Thanks.

The expression for the electric field is still incorrect. How do you figure the enclosed charge?

 

[lorenz0]

The expression for the electric field is still incorrect. How do you figure the enclosed charge?

Ah, I see, when considering the Gaussian surface I didn't account for all the charges inside it; $E(r)=\begin{cases}\frac{\lambda R_1}{\varepsilon_0 r} & R_1<r<R_2\\ \frac{\lambda (R_1-R_2+R_3)}{\varepsilon_0 r} & R_3<r<R_4\\ \frac{\lambda(R_1-R_2+R_3-R_4+R_5)}{\varepsilon_0 r} & r>R_5\end{cases}.$

 

[kuruman]

Still not right. You are convinced that the magnitude of the electric field from a conducting cylinder of radius $R_1$, bearing linear charge density $\lambda$, is $E=\frac{\lambda R_1}{\epsilon_0 r}$. I am not convinced that you are writing down the correct expression. Please use Gauss's law to convince me that it is correct or convince yourself that it is incorrect and find the correct expression. This applies to all the expressions in all regions.

As an aside, your equations in post #5 have a vector quantity $\vec E(r)$ on the left-hand side and scalar quantities on the right. You need to be consistent to avoid trouble.

 

[lorenz0]

Still not right. You are convinced that the magnitude of the electric field from a conducting cylinder of radius $R_1$, bearing linear charge density $\lambda$, is $E=\frac{\lambda R_1}{\epsilon_0 r}$. I am not convinced that you are writing down the correct expression. Please use Gauss's law to convince me that it is correct or convince yourself that it is incorrect and find the correct expression. This applies to all the expressions in all regions.

As an aside, your equations in post #5 have a vector quantity $\vec E(r)$ on the left-hand side and scalar quantities on the right. You need to be consistent to avoid trouble.

I mistook $\lambda$ for the **surface** charge density on the cylinder (so I had an additional $2\pi R_i$ factor on the right side of Gauss Law)!
$E(r)=\frac{\lambda}{2\pi\varepsilon_0 r}$ for $R_1<r<R_2$ or $R_3<r<R_4$ or $r>R_5$ since if we consider a coaxial cylindrical Gaussian surface we have $E(r)\cdot 2\pi r L=\frac{\lambda L}{\varepsilon_0}$ which implies $E(r)=\frac{\lambda}{2\pi\varepsilon_0 r}.$

 

[kuruman]

I think you now have all the ingredients to do this right.