Confidence Interval for Child's Weight Based on Television Watching

[mathmari]

Hey!

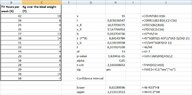
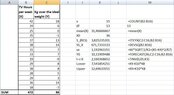
In a study at $15$ children at the age of $10$ years the number of hours of television watching per week and the pounds above or below the ideal body weight were determined (high positive values ​​= overweight).

1. Determine the simple linear regression equation by considering the weights above the ideal body weight as a dependent variable.
2. Perform a significance test for the slope of the regression line at significance level $\alpha = 5\%$ (using p-values).
3. Perform a significance test of the criterion F at significance level $\alpha = 0.05$ (using p-values).
4. Determine the confidence interval for the average weight in pounds for a child who watches television for $36$ hours a week and for a child who watches television for $30$ hours a week. Which confidence interval is greater and why?

I have done the following:

1. At the beginning I calculated the following:
   
   View attachment 9480
   
   Using these information we get:
   \begin{align*}&\nu =15 \\ &\overline{X}=\frac{\sum X}{\nu}=\frac{472}{15}=31.47 \\ &\overline{Y}=\frac{\sum Y}{\nu}=\frac{86}{15}=5.73 \\ &\hat{\beta}=\frac{\nu \sum \left (XY\right )-\left (\sum X\right )\left (\sum Y\right )}{\nu\sum X^2-\left (\sum X\right )^2}=\frac{15 \cdot 3356-472\cdot 86}{15\cdot 15524-472^2}=\frac{50340-40592}{232860-222784}=\frac{9748}{10076}=0.97 \\ & \hat{\alpha}=\overline{Y}-\hat{\beta}\cdot \overline{X}=5.73-0.97\cdot 31.47=5.73-30.5259=-24.80\end{align*}
   
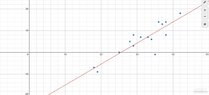
   Therefore the linear regression equation with dependent variable the kg over the ideal weights is: \begin{equation*}\hat{Y}=0.97X-24.80\end{equation*}
   
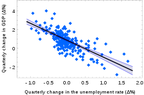
   The graph looks as follows:
   
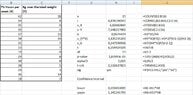
   View attachment 9482
2. We want to test the null hypothesis that the slope of the regression line is $0$.
   
   I found some notes and according to these I did the following:
   
   View attachment 9481 Since p-value < α (or |t| > t-crit) we reject the null hypothesis, and so we can’t conclude that the population slope is zero.
   
   Is this correct? (Wondering)
   
   But, according to these calculations we get an other slope than I got in the first question, or not? Here we have $b=0,91$ and in the first question I got $\hat{\beta}=0,97$.
   So have I done something wrong at the calculation of the linear regression equation? (Wondering)
   

 

[I like Serena]

[*] We want to test the null hypothesis that the slope of the regression line is $0$.

Hey mathmari!

Let's rephrase that... we want to test the alternative hypothesis that the slope of the regression line is not $0$. (Nerd)

I found some notes and according to these I did the following:

Since p-value < α (or |t| > t-crit) we reject the null hypothesis, and so we can’t conclude that the population slope is zero.

Is this correct?

Since we have a 2-sided test we need to compare the p-value with α/2.
If it is below - and see below for an apparent calculation mistake - then we conclude that the slope is significantly different from zero.
Or put otherwise, that there is a significant linear correlation between X and Y.
Note that we can never conclude that the population slope is 0. At best we do not have sufficient information to conclude that it is different. (Nerd)

But, according to these calculations we get an other slope than I got in the first question, or not? Here we have $b=0,91$ and in the first question I got $\hat{\beta}=0,97$.
So have I done something wrong at the calculation of the linear regression equation?

Looks as if there is a mistake.
I get different values for s_X and s_Y. I have s_X=6.92 and s_Y=7.648.
Perhaps the excel range was not set correctly? (Wondering)

 

[mathmari]

Since we have a 2-sided test we need to compare the p-value with α/2.
If it is below - and see below for an apparent calculation mistake - then we conclude that the slope is significantly different from zero.
Or put otherwise, that there is a significant linear correlation between X and Y.
Note that we can never conclude that the population slope is 0. At best we do not have sufficient information to conclude that it is different. (Nerd)

So do we have the following? (Wondering)

Since p-value < α/2 (or |t| > t-crit) we reject the null hypothesis, and so we conclude that the slope is significantly different from zero.

Looks as if there is a mistake.
I get different values for s_X and s_Y. I have s_X=6.92 and s_Y=7.648.
Perhaps the range was not set correctly? (Wondering)

Ah yes, I found my mistake at the commands at Excel.

Now I get:

View attachment 9484So now it is the same slope as I found in the first question! (Whew)

 

[I like Serena]

So do we have the following?

Since p-value < α/2 (or |t| > t-crit) we reject the null hypothesis, and so we conclude that the slope is significantly different from zero.

I've just noticed that you've used [M]=TDIST(x, df, tails=2)[/M] to calculate the p-value. If I'm not mistaken it means that the factor 2 has already been taken care of so that we can compare the p-value and α directly.

And yes, we conclude that the slope is significantly different from zero. (Nod)

Ah yes, I found my mistake at the commands at Excel.
Now I get:
So now it is the same slope as I found in the first question! (Whew)

Good! (Handshake)

 

[mathmari]

I've just noticed that you've used [M]=TDIST(x, df, tails=2)[/M] to calculate the p-value. If I'm not mistaken it means that the factor 2 has already been taken care of so that we can compare the p-value and α directly.

And yes, we conclude that the slope is significantly different from zero. (Nod)
Good! (Handshake)

Great!

Could you give me a hint for the question 3? What exactly is the criterion F? (Wondering)

 

[I like Serena]

Great!

Could you give me a hint for the question 3? What exactly is the criterion F?

You have just executed a t-test to test whether the slope is different from 0.
As I understand it, we can also do an F-test for the same thing.
An F-test tests whether 2 variances are different. The F-value is the ratio between those 2 variances. (Thinking)

 

[mathmari]

You have just executed a t-test to test whether the slope is different from 0.
As I understand it, we can also do an F-test for the same thing.
An F-test tests whether 2 variances are different. The F-value is the ratio between those 2 variances. (Thinking)

I used in Excel the "F-Test for the variances of two samples" and I got the following: View attachment 9485
Is this correct, i.e. did I give the correct inputs? (Wondering)

 

[I like Serena]

I used in Excel the "F-Test for the variances of two samples" and I got the following:

Is this correct, i.e. did I give the correct inputs?

I don't think so.
It appears you have compared the variances of the inputs and the outputs.
But that does not really say whether they are correlated or not does it? (Worried)

Perhaps we should search for what kind of F-test we can do within the context of a linear regression.
It should compare the 'explained' variance with the 'unexplained' variance. (Thinking)

 

[mathmari]

Perhaps we should search for what kind of F-test we can do within the context of a linear regression.
It should compare the 'explained' variance with the 'unexplained' variance. (Thinking)

The explained variance is the sum of the squared of the differences between each predicted Y-value and the mean of Y.

The unexplained variance is the sum of the squared of the differences between the Y-value of each ordered pair and each corresponding predicted Y-value.

Right? (Wondering) Is the F-value the fraction of these two values?

If yes, then we have the following:
\begin{equation*}F=\frac{\text{explained variance}}{\text{unexplained variance}}=\frac{632.0347}{190.2276}=3.32252\end{equation*}

(Wondering)

 

[mathmari]

Oh sorry, I forgot to upload the table:

View attachment 9490

 

[I like Serena]

The explained variance is the sum of the squared of the differences between each predicted Y-value and the mean of Y.

The unexplained variance is the sum of the squared of the differences between the Y-value of each ordered pair and each corresponding predicted Y-value.

Right?

Those are the sum-squared values, typically abbreviated as SSM and SSE.
To find the variances we still need to divide by the corresponding degrees-of-freedom (DFM and DFE) don't we? (Wondering)

Is the F-value the fraction of these two values?

If yes, then we have the following:
\begin{equation*}F=\frac{\text{explained variance}}{\text{unexplained variance}}=\frac{632.0347}{190.2276}=3.32252\end{equation*}

Yes, the F-value is that fraction.
But I think the numbers for the variances are not correct yet. (Worried)

 

[mathmari]

Those are the sum-squared values, typically abbreviated as SSM and SSE.
To find the variances we still need to divide by the corresponding degrees-of-freedom (DFM and DFE) don't we? (Wondering)Yes, the F-value is that fraction.
But I think the numbers for the variances are not correct yet. (Worried)

Oh ok!

So we have that DFM = p - 1, where p is the number of regression parameters, which is 2 in this case, and so we get DFM = 2-1=1, or not?

We also have that DFE = n - p, where n is the number of observations, and so we get DFE = 15 - 2 =13, or not?

(Wondering)

 

[I like Serena]

Oh ok!

So we have that DFM = p - 1, where p is the number of regression parameters, which is 2 in this case, and so we get DFM = 2-1=1, or not?

We also have that DFE = n - p, where n is the number of observations, and so we get DFE = 15 - 2 =13, or not?

Yep. (Nod)

 

[mathmari]

Yep. (Nod)

So using the table of post #10 we get
\begin{align*}&SSM=632.0347 \\ &DFM=2-1=1 \\ &SSE=190.2276 \\ &DFE=15-2=13 \\ &MSM=\frac{SSM}{DFM}=\frac{632.0347}{1}=632.0347 \\ &MSE=\frac{SSE}{SFE}=\frac{190.2276}{13}=14.6329 \\ &F=\frac{MSM}{MSE}=\frac{632.0347}{14.6329}=43.1927\end{align*}

Now we have to find the confidence interval for the test statistic with $\alpha=0.05$, right? We look in the F-table at the $0.05$ entry for $1$ df in the numerator and $13$ df in the denominator.

Using the R program and compiling the function qf(0.95, 1, 13) we get 4.667193.

Is so far everything correct?

How is the confidence interval defined with these data? (Wondering)

 

[I like Serena]

So using the table of post #10 we get
\begin{align*}&SSM=632.0347 \\ &DFM=2-1=1 \\ &SSE=190.2276 \\ &DFE=15-2=13 \\ &MSM=\frac{SSM}{DFM}=\frac{632.0347}{1}=632.0347 \\ &MSE=\frac{SSE}{SFE}=\frac{190.2276}{13}=14.6329 \\ &F=\frac{MSM}{MSE}=\frac{632.0347}{14.6329}=43.1927\end{align*}

Now we have to find the confidence interval for the test statistic with $\alpha=0.05$, right? We look in the F-table at the $0.05$ entry for $1$ df in the numerator and $13$ df in the denominator.

Using the R program and compiling the function qf(0.95, 1, 13) we get 4.667193.

Is so far everything correct?

I have found the F-value 42.967. That is more or less the same F-value. Good.
The difference is probably caused by early rounding.

And you have found a critical F-value.
But shouldn't we find a p-value to compare with $\alpha$? And draw a conclusion? (Wondering)

How is the confidence interval defined with these data?

For the F-test you mean?
The F-test is a 1-sided test in this case, and generally a confidence interval belongs to a 2-sided test.
So I don't think we should calculate a confidence interval in this case. (Thinking)

 

[mathmari]

I have found the F-value 42.967. That is more or less the same F-value. Good.
The difference is probably caused by early rounding.

And you have found a critical F-value.
But shouldn't we find a p-value to compare with $\alpha$? And draw a conclusion? (Wondering)

So shouldn't I have calculated that F value? How do we calculate the p value? (Wondering)

 

[I like Serena]

So shouldn't I have calculated that F value? How do we calculate the p value?

You found a formula in R to calculate the critical F-value from $\alpha$.
Isn't there a simular formula to calculate the p-value from the F-value? (Wondering)

 

[mathmari]

You found a formula in R to calculate the critical F-value from $\alpha$.
Isn't there a simular formula to calculate the p-value from the F-value? (Wondering)

Using the function pf(42.967, 1, 13, lower.tail=F) we get 1.839458e-05.

Is the function correct? (Wondering)

 

[I like Serena]

Using the function pf(42.967, 1, 13, lower.tail=F) we get 1.839458e-05.

Is the function correct?

Yep.
Previously you used the t-test to find the p-value for the slope. Now we used the F-test. The result should be the same shouldn't it? Is it? (Wondering)

 

[mathmari]

Yep.
Previously you used the t-test to find the p-value for the slope. Now we used the F-test. The result should be the same shouldn't it? Is it? (Wondering)

Ah yes, they are the same!

So we compare now the p-value ith $\alpha$, or not? Sodo we have the following? (Wondering)

Since p-value < α we reject the null hypothesis, and so we conclude that the slope is significantly different from zero. As for the question 4, how is the confidence interval defined, which formula do we use? (Wondering)

 

[I like Serena]

Ah yes, they are the same!

So we compare now the p-value ith $\alpha$, or not? Sodo we have the following? (Wondering)

Since p-value < α we reject the null hypothesis, and so we conclude that the slope is significantly different from zero.

Yep. (Nod)

As for the question 4, how is the confidence interval defined, which formula do we use?

We are looking for the confidence interval of a point estimate in a simple linear regression.
I found a formula here, here and here.
Wikipedia gives a confidence band formula for the same thing. (Thinking)

 

[mathmari]

We are looking for the confidence interval of a point estimate in a simple linear regression.
I found a formula here, here and here.
Wikipedia gives a confidence band formula for the same thing. (Thinking)

So do we have the following? (Wondering)

View attachment 9499

That would mean that the confidence interval is $[7.541854251, \ 12.69633551]$.

Is that correct? (Wondering)

 

[I like Serena]

So do we have the following? (Wondering)
That would mean that the confidence interval is $[7.541854251, \ 12.69633551]$.

Is that correct? (Wondering)

I didn't check the numbers, but the approach seems to be correct.
Still, didn't the question ask for a child who watches television for 30 hours a week as well? And the corresponding confidence interval? (Wondering)

 

[mathmari]

I didn't check the numbers, but the approach seems to be correct.
Still, didn't the question ask for a child who watches television for 30 hours a week as well? And the corresponding confidence interval? (Wondering)

For that we do the same just replacing the 36 hours by 30 hours, or not? (Wondering)

 

[I like Serena]

For that we do the same just replacing the 36 hours by 30 hours, or not?

I guess so, assuming your previous approach was correct which seems plausible. (Thinking)

 

[mathmari]

I guess so, assuming your previous approach was correct which seems plausible. (Thinking)

Applying thesame methodas before I get that the confidence interval for the case of 30 hours is $[2.130030132, \ 6.498790828]$.

Determine the confidence interval for the average weight in pounds for a child who watches television for $36$ hours a week and for a child who watches television for $30$ hours a week. Which confidence interval is greater and why?

By greater it is meant larger values not bigger width, right?

If yes, the greater confidence interval is the first one, for the case of 36 hours. How do we justify that? (Wondering)

 

[I like Serena]

Applying thesame methodas before I get that the confidence interval for the case of 30 hours is $[2.130030132, \ 6.498790828]$.

Looking at your graph in post #1, that looks about right. (Nod)

By greater it is meant larger values not bigger width, right?

If yes, the greater confidence interval is the first one, for the case of 36 hours. How do we justify that?

I believe they mean a greater range of the confidence interval. The range is the upper bound minus the lower bound.
Either way, that is also the confidence interval of 36 hours.

The wiki article explains that the range of the confidence interval has 2 parts:

1. The error due to uncertainty in estimated slope ($\hat\beta_1$) and y-intersection ($\hat\beta_0$). This error is the least close to the center, and grows bigger away from the center.
2. The error due to scattering from unexplained sources, which is assumed to be normally distributed with equal variance everywhere.

They also show a picture with the confidence band that has a hyperbolic shape (unrelated to this problem):
View attachment 9502
As you can see, the band is narrowest at the mean X-value, and grows wider in both positive and negative directions.

And indeed, 30 hours is closer to the mean X-value of 31.47 than 36 hours. (Thinking)