Haku
- 30
- 1
- Homework Statement
- Defining the existence of a limit
- Relevant Equations
- Limits
If you are told something holds if the limit exists, and given a function f (specifically not piecewise defined), is it enough to show that the limit as x approaches c = the function evaluated at c?
With a piecewise defined function, it is easy to check both sides of a potential discontinuity, by using each part of the defined function, i.e. from either side of the potential discontinuity.
For example:

In this definition, the j-th partial derivative of f at x0 exists if that limit exists.
Does it exist if it is equal to something not infinity? Or would I need to be more rigorous and show the limits from either side exist and are all equal to each other?
An application of this definition is used in the following example:
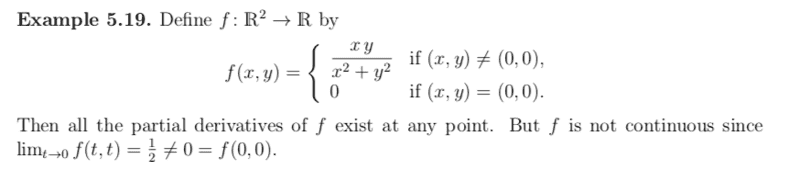
Where I checked that all partial derivatives exist via the above definition, but when checking, for example, j-th partial derivatives at (x, y) = (0, 0) for j = 1, you just use that definition above and get that the limit = 0. And by my lecturer in class, that was sufficient.
But, was that enough? Because since we are using limits (and in analysis), rather than just assuming it exists and plugging in for specific values, wouldn't you have to actually prove that the limit exists first? Rather than just show that the limit as t approaches 0 of f(0, 0) = function evaluated at (0, 0) = 0?
Thanks.
With a piecewise defined function, it is easy to check both sides of a potential discontinuity, by using each part of the defined function, i.e. from either side of the potential discontinuity.
For example:
In this definition, the j-th partial derivative of f at x0 exists if that limit exists.
Does it exist if it is equal to something not infinity? Or would I need to be more rigorous and show the limits from either side exist and are all equal to each other?
An application of this definition is used in the following example:
Where I checked that all partial derivatives exist via the above definition, but when checking, for example, j-th partial derivatives at (x, y) = (0, 0) for j = 1, you just use that definition above and get that the limit = 0. And by my lecturer in class, that was sufficient.
But, was that enough? Because since we are using limits (and in analysis), rather than just assuming it exists and plugging in for specific values, wouldn't you have to actually prove that the limit exists first? Rather than just show that the limit as t approaches 0 of f(0, 0) = function evaluated at (0, 0) = 0?
Thanks.