Confused about force body diagram for 2 body collision

[PhysicsQuestions]

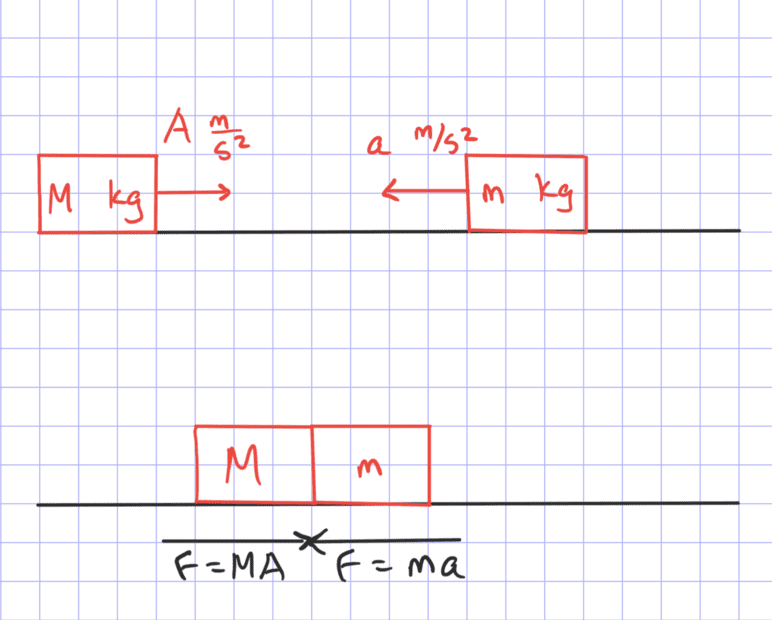
I'm trying to understand Newton's third law in the context of collisions. Assume that one body has mass M kg and is traveling in the positive x direction with acceleration A m/s^2. Assume that the second body has mass m kg and is traveling in the negative x direction with acceleration a m/s^2. At the moment of collision (elastic or inelastic), when you measure the force exerted on each object, both bodies will experience the same force. Is this force going to be F = MA + ma and how would you go about drawing this force body diagram? If the total force were F = MA + ma, would you just have that arrow going from the first body to the second and vice versa? Or would you separate out the arrows into F = MA and F = ma?

 

[PeroK]

The acceleration of each mass must be due to some external forces. These are not directly related to the equal and opposite forces between the objects during a collision.

Normally a collision is studied using the relative velocity between the objects. There is no need to have external forces accelerating the objects towards each other.

 

[Nugatory]

You have specified that both objects are accelerating towards one another, but that is not enough information: we need initial velocities as well as the accelerations, and we need the duration of the collision.

To see this, consider that even if the accelerations were zero (the two objects are moving towards one another at a constant speed) there would be a non-zero force, greater if the speeds are greater so we need the initial speeds as well as the acceleration. We also need the duration of the collision because the longer it lasts the smaller the force needed to produce the same effect.

 

[PhysicsQuestions]

You have specified that both objects are accelerating towards one another, but that is not enough information: we need initial velocities as well as the accelerations, and we need the duration of the collision.

To see this, consider that even if the accelerations were zero (the two objects are moving towards one another at a constant speed) there would be a non-zero force, greater if the speeds are greater so we need the initial speeds as well as the acceleration. We also need the duration of the collision because the longer it lasts the smaller the force needed to produce the same effect.

If we assign numbers for the sake of clarity, let's say the left block has mass 10 kg, initial velocity 4 m/s, and acceleration 4.5 m/s^2. Let's say the right block has mass 20 kg, initial velocity -4 m/s, and acceleration -4.5 m/s^2. And finally assume the collision lasts .5 seconds.

If they start at 0 and 2 meters, they will meet at the 1 meter mark. The 10kg block will have velocity $\sqrt{4^2 + 2(4.5)(1)} = 5 m/s$ and the 20 kg block will have velocity -5 m/s. How can we use this information to figure out the force as you suggested?

 

[Nugatory]

How can we use this information to figure out the force as you suggested?

We calculate the change of speed of either object during the collision (from conservation of energy and momentum and whether the collision is elastic or not - somewhat simpler if it is), divide that change by the elapsed time to get the average acceleration, and then F=ma gives us the force acting on that object to produce that change.

 

[PhysicsQuestions]

We calculate the change of speed of either object during the collision (from conservation of energy and momentum and whether the collision is elastic or not - somewhat simpler if it is), divide that change by the elapsed time to get the average acceleration, and then F=ma gives us the force acting on that object to produce that change.

This explanation makes a lot of sense thanks! When drawing the free body diagram, should I draw just two arrows then? One from the left to the right and one from the right to the left, both with the magnitude of the force calculated above?

 

[vanhees71]

If the forces acting is only due to their mutual interaction, then Newton's 3rd Law holds. This example seems to be for one-dimensional motion. That's why we work with only one component of the vectors. So the equation of motion for the bodies read
$$m a=F_1, \quad M A=F_2.$$
Then Newton's 3rd Law tells you that
$$F_2=-F_1.$$
The most important conclusion is that total momentum is conserved. Indeed
$$m a+MA = F_1+F_2=0.$$
But $a= \dot{v}$ and $A=\dot{V}$. So you can integrate this equation to
$$m v+MV = P=\text{const}.$$
It is important to realize that the two forces in Newton's 3rd Law act on the two different bodies, respectively!