Confused about tension in strings

[Gustav3497]

Hello! I'm just having trouble understanding the logic about tension in strings.

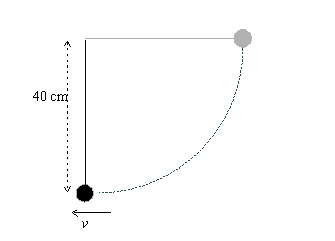
m = 5[kg]
v = 2.8 [m/s]
g = 10 [m/(s^2)]
String in massless and air friction is negligible

The question is what the tension in the string is when the ball is in the bottom position. My reasoning is that the string tension only should consist of the weaker force, the gravitational force (F= mg). However, the solution says that the string tension is the sum of both the centripetal and gravitational force:

F_tension=m(v^2)/r + mg = 150 [N]

I'm having trouble buying that logic, because in a tug of war the rope tension is limited by the force with which the weaker team pulls. So why is that not the case here? Why is the tension the sum of both forces in opposite directions, and not equal to the weaker force, the gravitational one?

Thanks in advance!

 

[scottdave]

What keeps the ball from continuing in a straight line? The tension. Take the same situation out into space, or just whirl it in a horizontal circle. If the ball is traveling with the same tangential velocity (v), what is the tension in the string?

 

[Nugatory]

The net force on the ball is the sum of the two forces acting on it: gravity and the tension in the string. What is the acceleration of the ball? Plug that into $F=ma$ and solve for the net force and hence the tension.

Your tug-of-war comparison is confusing you. You should be approaching that problem in the same way: what force is required to produce the observed acceleration? The "strength" of a team is determined by the maximum force between their feet and the ground.

 

[Gustav3497]

What keeps the ball from continuing in a straight line? The tension. Take the same situation out into space, or just whirl it in a horizontal circle. If the ball is traveling with the same tangential velocity (v), what is the tension in the string?

Well in that case it'd just be the centripetal force that is the tension. What I'm having trouble to grasp is why the tension in the string consists of both F_mg and F_c. F_c pulls the ball to the center, and mg pulls it away from the center. The forces act in opposite directions. If we'd have that situation in a tug of war, where one team pulls with 100 N, (as without centripetal force pulling the string towards the center) and the other with 50 N in the opposite direction (in this case the F_mg pulls the string away from the center), the string tension would still only be equivelant to the weaker force, 50 N. That is what confuses me.

 

[Gustav3497]

The net force on the ball is the sum of the two forces acting on it: gravity and the tension in the string. What is the acceleration of the ball? Plug that into $F=ma$ and solve for the net force and hence the tension.

Your tug-of-war comparison is confusing you. You should be approaching that problem in the same way: what force is required to produce the observed acceleration? The "strength" of a team is determined by the maximum force between their feet and the ground.

But I why isn't the tug of war solution applicable to this problem? The two forces each pull on a rope, and the tension of the rope can't be greater than the weakest force pulling?

 

[Chestermiller]

Have you bothered to draw a free body diagram and then to apply Newton's 2 nd law to write down the force balance?

 

[Nugatory]

But I why isn't the tug of war solution applicable to this problem? The two forces each pull on a rope, and the tension of the rope can't be greater than the weakest force pulling?

It does turn out that in the tug of war case the tension in the rope will be equal to the force exerted on it by the weaker team (which is also the force exerted on the rope by the stronger team as long as neither team is being dragged across the ground - if this is not completely clear to you, stop right now, draw a complete free-body diagram showing all four third-law pairs) but that's not the right way of thinking about it and it's an accident that it leads to the right answer in that particular problem.

Instead, look at the net force (in general, determined from $F=ma$ but trivially zero if the acceleration is zero, as in the tug-of-war case) on whatever the end of the rope is attached to. The tension on the rope is whatever it takes to make the net force come out right. That's why I asked what the acceleration of the ball is. Draw the free-body diagram for the tug-of-war case and the ball, see if it starts to make sense.

 

[scottdave]

But I why isn't the tug of war solution applicable to this problem? The two forces each pull on a rope, and the tension of the rope can't be greater than the weakest force pulling?

This is not a static system. You should draw a free body diagram, as @Chestermiller suggested.
Consider this different situation: A 1 kg mass hangs stationary from a pulley with a brake on it. With enough force from the brake, it hangs motionless. The mass "pulls down" with 9.8 Newtons of force on the string. The string has 9.8 Newtons of tension. The pulley "pulls up" with 9.8 Newtons of force.

Now suppose the brake is loosened and it starts to slip. Let's say the pulley can now pull up with only 8.8 Newtons of force. What is happening in that situation?

How about another one? The mass hangs from the ceiling of an elevator lift. The elevator starts accelerating upward at 1 m/s². What happens to the forces and the tensions. Once you have a handle on those, then the swinging ball should be a little easier to understand.

 

[Gustav3497]

Thanks all of you for your time and effort! It finally clicked! Taking a break and looking at your replies helped to finally clear things up. :)