- #1
Anchovy
- 99
- 2
I have some confusion over some diagrams involved in proton decays in SU(5). I've seen a few like this that look weird to me. Here is one I found where the colored Higgs triplet does the job:
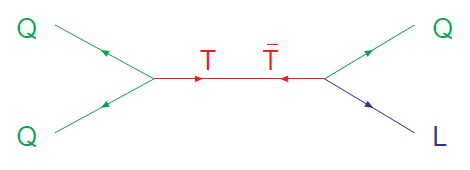
Straight away I don't know what to make of this because I've only ever seen diagrams where fermions are connected by one exchange boson. Here there are two, the [itex]T[/itex] and [itex]\overline{T}[/itex].
If I'm not mistaken, [itex]T[/itex] is meant to have a charge of -1/3 and [itex]\overline{T}[/itex] has +1/3. So if I specify the left hand side quarks with two of the three (uud) proton constituents, [itex]u^{+2/3}[/itex] and [itex]d^{-1/3}[/itex], then the charge from those quarks going into the left vertex is +1/3 overall. So there should be a [itex]\overline{T}[/itex] coming out of that vertex since it also has charge +1/3. But then the arrows look wrong since the arrows on the u, d should be pointing to the right?
Anyway, then the right hand side vertex would have [itex]\overline{T}[/itex] going in, so then the leading decay mode in this situation ([itex]p \rightarrow K^{+} \overline{\nu}[/itex]) would invove the Q on the right hand side being an [itex]\overline{s}[/itex] with charge of +1/3 (with the spectator u quark (which isn't shown) combining with the [itex]\overline{s}[/itex] to produce the [itex]K^{+}[/itex]), and the antilepton L being neutral, ie. [itex]\overline{\nu}[/itex].
So the diagram seems to make sense if I ignore one of the bosons. Has whoever drew this diagram combined two different interactions into the same diagram here, and if so, do the arrows really make sense? Or am I misinterpreting the [itex]T[/itex] / [itex]\overline{T}[/itex] line in this diagram?
Here's another one, this time a SUSY diagram:
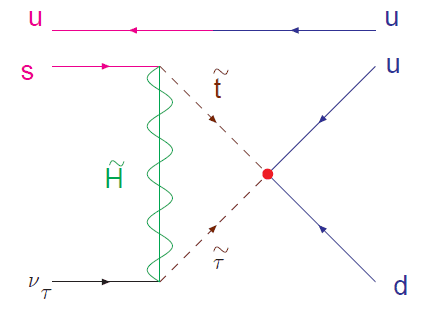
The [itex]u^{+2/3}[/itex] and [itex]d^{-1/3}[/itex] put an overall +1/3 charge into the red dot vertex, the anti-stop (anti based on the arrow direction) has a -2/3 charge and the anti-stau a +1 charge, so the red dot vertex has overall +1/3 coming out of it too. So far so good.
Then we get to the vertices with the Higgsino. At the upper vertex, there's a -2/3 charge going in from the stop, and the anti-strange quark has charge +1/3, so the Higgsino must be a -1 charge (ie. it must be the anti-particle of the superpartner to the [itex]H^{+}[/itex] in the [itex](H^{+}, H^{0})[/itex] SU(2) doublet within the SU(5) [itex]\psi_{\textbf{5}}[/itex] multiplet). Similarly the +1 of the anti-stau and the -1 of the anti-Higgsino cancel to give the electrically neutral antineutrino.
--> Assuming the above interpretation is correct, my issues with this are:
1) Is there a reason why this diagram, meant to indicate proton decay, is set up to be read left-to-right rather than right-to-left?
2) I believe this decay is described by what gets referred to as a 'dimension 5' operator. I think that refers to what is happening at the red dot. However, I don't understand the '5' part. There are only 4 fields involved [itex](u, d, \tilde{t},\tilde{\tau})[/itex]. What is '5-dimensional' about this situation?
Straight away I don't know what to make of this because I've only ever seen diagrams where fermions are connected by one exchange boson. Here there are two, the [itex]T[/itex] and [itex]\overline{T}[/itex].
If I'm not mistaken, [itex]T[/itex] is meant to have a charge of -1/3 and [itex]\overline{T}[/itex] has +1/3. So if I specify the left hand side quarks with two of the three (uud) proton constituents, [itex]u^{+2/3}[/itex] and [itex]d^{-1/3}[/itex], then the charge from those quarks going into the left vertex is +1/3 overall. So there should be a [itex]\overline{T}[/itex] coming out of that vertex since it also has charge +1/3. But then the arrows look wrong since the arrows on the u, d should be pointing to the right?
Anyway, then the right hand side vertex would have [itex]\overline{T}[/itex] going in, so then the leading decay mode in this situation ([itex]p \rightarrow K^{+} \overline{\nu}[/itex]) would invove the Q on the right hand side being an [itex]\overline{s}[/itex] with charge of +1/3 (with the spectator u quark (which isn't shown) combining with the [itex]\overline{s}[/itex] to produce the [itex]K^{+}[/itex]), and the antilepton L being neutral, ie. [itex]\overline{\nu}[/itex].
So the diagram seems to make sense if I ignore one of the bosons. Has whoever drew this diagram combined two different interactions into the same diagram here, and if so, do the arrows really make sense? Or am I misinterpreting the [itex]T[/itex] / [itex]\overline{T}[/itex] line in this diagram?
Here's another one, this time a SUSY diagram:
The [itex]u^{+2/3}[/itex] and [itex]d^{-1/3}[/itex] put an overall +1/3 charge into the red dot vertex, the anti-stop (anti based on the arrow direction) has a -2/3 charge and the anti-stau a +1 charge, so the red dot vertex has overall +1/3 coming out of it too. So far so good.
Then we get to the vertices with the Higgsino. At the upper vertex, there's a -2/3 charge going in from the stop, and the anti-strange quark has charge +1/3, so the Higgsino must be a -1 charge (ie. it must be the anti-particle of the superpartner to the [itex]H^{+}[/itex] in the [itex](H^{+}, H^{0})[/itex] SU(2) doublet within the SU(5) [itex]\psi_{\textbf{5}}[/itex] multiplet). Similarly the +1 of the anti-stau and the -1 of the anti-Higgsino cancel to give the electrically neutral antineutrino.
--> Assuming the above interpretation is correct, my issues with this are:
1) Is there a reason why this diagram, meant to indicate proton decay, is set up to be read left-to-right rather than right-to-left?
2) I believe this decay is described by what gets referred to as a 'dimension 5' operator. I think that refers to what is happening at the red dot. However, I don't understand the '5' part. There are only 4 fields involved [itex](u, d, \tilde{t},\tilde{\tau})[/itex]. What is '5-dimensional' about this situation?