Grizzly_1
- 7
- 3
- TL;DR Summary
- The coil diagram provided seems to contradict itself in the next diagram.
Hello all, I am currently studying for a physics a-level qualification in the UK, I use the AQA specification and I am having trouble understanding this image representing a scenario I found in my textbook. The first image in the three part diagram shows this rotating coil and to me, it makes absolutely no sense how from that image, you arrive at the side view in the second picture (I understand the physics of the side view image). Is this a poorly drawn diagram? or am I missing something? As to me it appears that not only is the coil at an angle to the field but also the axis itself is at an angle to the field, wouldn't this fundamentally change how the magnetic field interacted with it? How can the first image turn into the second if the axis isn't aligned at pi/2 rads to the magnetic field?
Any guidance on this is much appreciated, I am thoroughly confused.
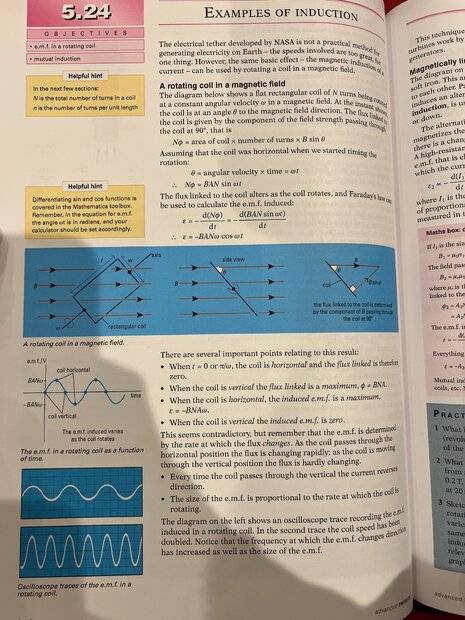
Any guidance on this is much appreciated, I am thoroughly confused.
Last edited: