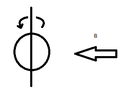Confusing Issue with Lenz's Law

[Ackbach]

In my AP Physics B class that I'm teaching, we arrived at Lenz's Law, and had difficulty with Conceptual Example 21-4 (e), located on page 588 of Giancoli's Physics, 6th Ed., which goes like this:

A closed conducting circle of wire is lying the plane of the page (or screen), and there is a magnetic $\mathbf{B}$ field pointing to the left, in the plane of the page (or screen). Hence, there is initially zero magnetic flux through the area of the circle. Then we rotate the loop about a vertical axis (in the plane of the page) by pulling the left side towards us out of the page and pushing the right side into the page. In which direction is the induced current: clockwise or counter-clockwise? See the following picture for an illustration of the physical situation.

View attachment 653

There are several ways to think about this. Probably the most intuitive method is the conservation of energy approach: the induced current must produce a magnetic field which does not, in turn, contribute to the magnetic force already on the loop. If it did, we would have a positive feedback loop situation, and we could get a perpetual motion machine. Therefore, the current must produce a magnetic field in the area of the loop that opposes the existing magnetic field. Hence, the current must be counterclockwise.

However, the standard method of thinking about this problem is Lenz's Law, which states that a current induced by a changing magnetic flux must oppose that change. Now the magnetic flux we define to be $\Phi_{B}=BA\cos(\theta)$, where $\theta$ is defined to be the angle between the normal vector (which one?!?) and the magnetic field. If we say that the normal vector is initially pointing into the page, then the angle between the normal and the magnetic field is decreasing, the $\cos(\theta)$ is increasing (going from $0$ to $1$), and hence the current must generate a magnetic field that opposes the existing magnetic field. Hence, it must be counterclockwise. This agrees with the previous result.

But now, suppose we define the normal vector to be out of the page. The angle $\theta$ would be getting larger (more obtuse), and hence the $\cos(\theta)$ would be getting more negative. This was the situation that was confusing me in class. If the flux is getting more negative, then the induced current must be trying to make the flux less negative. Hence, the induced current must be trying to make the flux more positive. Which current direction would make that happen? Here you use the right-hand rule to fix the problem: if the current were to go counter-clockwise, your right hand would be curling around in that direction, and your thumb would point out of the page in the same direction as the normal force. That's positive. But, if you had a clockwise current, your thumb would point into the page, which is negative according to the way you defined the normal force.

So, counter-clockwise it is, then. Too bad that neither Giancoli nor Holt Physics explains this. I'll have to double-check Young and Freedman as well as Serway for calc-based books when I get back to school.

 

[MarkFL]

I have my old calculus based physics textbook which is Serway's Fourth Edition of "Physics For Scientists and Engineers" and on page 914, section 31.3 it states:

31.3 LENZ'S LAW

The direction of the induced emf and induced current can be found from Lenz's law (developed by the German physicist Heinrich Lenz (1804-1865)), which can be stated as follows:

The polarity of the induced emf is such that it tends to produce a current that will create a magnetic flux to oppose the change in magnetic flux through the loop.

That is, the induced current tends to keep the original flux through the circuit from changing. The interpretation of this statement depends on the circumstances. As we shall see, this law is a consequence of the law of conservation of energy.

In order to obtain a better understanding of Lenz's law, let us return to the example of a bar moving to the right on two parallel rails in the presence of a uniform magnetic field directed into the paper. As the bar moves to the right, the magnetic flux through the circuit increases with time since the area of the loop increases. Lenz's law says that the induced current must be in a direction so that the flux it produces opposes the change in the external magnetic flux. Since the flux due to the external field is increasing into the paper, the induced current, if it is to oppose the change, must produce a flux out of the paper. Hence, the induced current must be counterclockwise when the bar moves to the right to give a counteracting flux out of the paper in the region inside the loop. (Use the right-hand rule to verify this direction.) On the other hand, if the bar is moving to the left, the magnetic flux through the loop decreases with time. Since the flux is into the paper, the induced current has to be clockwise to produce a flux into the paper inside the loop. In either case, the induced current tends to maintain the original flux through the circuit.

Let us look at this situation from the viewpoint of energy considerations. Suppose that the bar is given a slight push to the right. In the above analysis, we found that this motion leads to a counterclockwise current in the loop. Let us see what happens if we assume that the current is clockwise. For a clockwise current $I$, the the direction of the magnetic force on the sliding bar would be to the right. This force would accelerate the rod and increase its velocity. This, in turn, would cause the area of the loop to increase more rapidly, thus increasing the induced current, which would increase the force, which would increase the current, which would . . . . In effect, the system would acquire more energy with no additional input energy. This is clearly inconsistent with all experience and with the law of conservation of energy. Thus, we are forced to conclude that the current must be counterclockwise.

Consider another situation, one in which a bar magnet is moved to the right toward a stationary loop of wire. As the magnet moves to the right toward the loop, the magnetic flux through the loop increases with time. To counteract this increase in flux to the right, the induced current produces a flux to the left.

Note that the magnetic field lines associated with the induced current opposes the motion of the magnet. Therefore the left face of the current loop is a north pole and the right face is a south pole.

On the other hand, if the magnet were moving to the left, its flux through the loop, which is toward the right, would decrease with time. Under these circumstances, the induced current in the loop would be in a direction so as to set up a field through the loop directed from left to right in an effort to maintain a constant number of flux lines. In this case the left face of the loop would be a south pole and the right face would be a north pole.

 

[Ackbach]

Giancoli, so far, seems to be the only physics book, calc-based or algebra-based, that has this conceptual example in it. I have not examined the end-of-chapter problems closely, but the following physics texts all lack this example in the text proper: Serway 4th Ed., Young and Freedman 9th Ed., Cutnell and Johnson 6th Ed., Halliday and Resnick 5th ed., and Holt 2002 Ed. I even examined my copy of Jackson's Classical Electrodynamics, 3rd Ed., but Lenz's Law gets very little treatment there. A look on Amazon reveals that Griffiths'sIntroduction to Electrodynamics, 3rd. Ed., does not have this example either.

 

[MarkFL]

I dug out my copy of The Electromagnetic Field by Albert Shadowitz, and in Chapter 11 "Maxwell's Equations", section 1 "Faraday's Law", page 396, it states:

5. Lenz's law The minus sign is Faraday's law, \(\displaystyle V=-\frac{d\Phi}{dt}\), gives the direction of the induced voltage. In figure 11-10$a$ let the circle represent a circuit in which a voltage induced by a changing \(\displaystyle \text{B}_{\text{ext}}\). Suppose \(\displaystyle \text{B}_{\text{ext}}\) is out of the page. The the area of the circle is represented by a vector which is out of the page. If \(\displaystyle \text{B}_{\text{ext}}\) increases, a voltage will be induced in the circuit, and this will cause a current to flow. A CW current flow would itself produce a \(\displaystyle \text{B}_{\text{ind}}\), within the circle, which is directed into the page; such a current would tend to oppose the increase of \(\displaystyle \text{B}_{\text{ext}}\) out of the page. Lenz's law says that the induced voltage would be CW, in order that the current should minimize the change in \(\displaystyle \text{B}_{\text{ext}}\). That is the meaning of the minus sign in Faraday's law. In figure 11-10$b$ \(\displaystyle \text{B}_{\text{ext}}\) is again outward, but now it is decreasing. Then the sign of $V$ is such as to produce \(\displaystyle \text{I}_{\text{ext}}\), here CCW, which produces a \(\displaystyle \text{B}_{\text{ind}}\) in the outward sense, to minimize the decrease.​

 

[Ackbach]

I dug out my copy of The Electromagnetic Field by Albert Shadowitz, and in Chapter 11 "Maxwell's Equations", section 1 "Faraday's Law", page 396, it states:

5. Lenz's law The minus sign is Faraday's law, \(\displaystyle V=-\frac{d\Phi}{dt}\), gives the direction of the induced voltage. In figure 11-10$a$ let the circle represent a circuit in which a voltage induced by a changing \(\displaystyle \text{B}_{\text{ext}}\). Suppose \(\displaystyle \text{B}_{\text{ext}}\) is out of the page. The the area of the circle is represented by a vector which is out of the page. If \(\displaystyle \text{B}_{\text{ext}}\) increases, a voltage will be induced in the circuit, and this will cause a current to flow. A CW current flow would itself produce a \(\displaystyle \text{B}_{\text{ind}}\), within the circle, which is directed into the page; such a current would tend to oppose the increase of \(\displaystyle \text{B}_{\text{ext}}\) out of the page. Lenz's law says that the induced voltage would be CW, in order that the current should minimize the change in \(\displaystyle \text{B}_{\text{ext}}\). That is the meaning of the minus sign in Faraday's law. In figure 11-10$b$ \(\displaystyle \text{B}_{\text{ext}}\) is again outward, but now it is decreasing. Then the sign of $V$ is such as to produce \(\displaystyle \text{I}_{\text{ext}}\), here CCW, which produces a \(\displaystyle \text{B}_{\text{ind}}\) in the outward sense, to minimize the decrease.​

Your first example is with a changing $\mathbf{B}$ field, which all the books have, pretty much. They will also often have the area of the current loop increasing or decreasing. But the flux is defined as $\Phi_{B}=BA\cos(\theta)$, so a changing angle between the $\mathbf{B}$ field and the normal to the surface will also change the flux, thus triggering Lenz's Law. Is your second example about a changing angle? It's a little hard for me to tell without seeing the accompanying figures.

 

[MarkFL]

It doesn't state how the field in changing, and no metion of a changing angle is given, only that the field is increasing in the first example, and decreasing in the second. I will draw sketches of the figures in the book tonight for clarity.

 

[Ackbach]

It doesn't state how the field in changing, and no metion of a changing angle is given, only that the field is increasing in the first example, and decreasing in the second. I will draw sketches of the figures in the book tonight for clarity.

Please don't bother - I think I have a pretty good handle on the changing $\mathbf{B}$ case, and the changing area case. And, now that I talked it over with my father, a good handle on the changing angle case (hence the writeup). The books have those examples, anyway.