Confusion about special case of Jacobian

[nomadreid]

TL;DR Summary

An author gives a definition of a Jacobian which is probably a special case of the usual Jacobian matrix, but I don't see it.

I am used to the usual definition of the Jacobian (when the talk is about derivatives) as the Jacobian matrix for multi-valued functions. However, in the 1995 edition of the introductory book "Basic Training in Mathematics: A fitness program for science students" on page 45 , equations 2.2.22 and 2.2.12 , the author R. Shankar defines the Jacobian as follows,

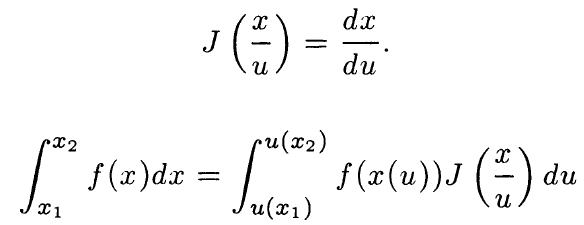
I am not sure how the two definitions correspond. If it is blindingly obvious, then my apologies but I would be very grateful if one could spell it out for me anyway. Thanks in advance.

 

[mathwonk]

thats the usual n variable jacobian for n=1, isn't it?

 

[nomadreid]

thats the usual n variable jacobian for n=1, isn't it?

Thanks, mathwonk. Ihat is, just the derivative. why would one label the simple derivative the Jacobian even if it is the degenerate case? Like referring to points as lines, because they are degenerate lines. If there is nothing hidden behind this besides perhaps wanting to perhaps later generalize it, then my question was trying to read between the lines when there was nothing to read, leaving me looking a bit foolish. In that case, the thread ends with my thanks.