Rikudo
- 120
- 26
- Homework Statement
- A mass m1 hits a stick (it has mass m2) at its end with velocity v0. After the collision, the stick both slides horizontally with velocity v2' and rotates. Find the angular velocity!
- Relevant Equations
- Linear momentum and angular momentum
I am currently reading David Morin book and found this statement :
##\,\,\,\,\,\,\,\,## "It is important to remember that you are free to choose your origin from the legal possibilities of fixed points or the CM"
Is it really alright to choose the center of a rigid body as an origin even though this body is fixed to a point? because when solving the problem above, I found that both methods yield different result.
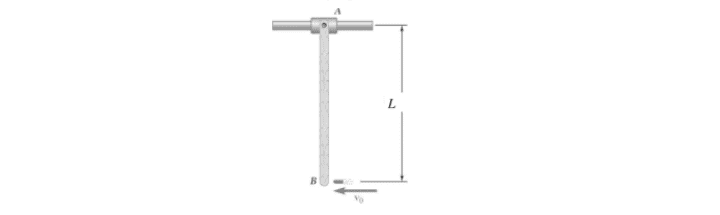
Here is my attempt
First, we need to calculate its Linear momentum. (This will be useful when we set the fixed point as an origin)
$$m_1\,V_0\,=\,m_2\,V'_2$$
##1.##Now, If I use the center of the stick as the origin, the angular momentum will be like this :
$$m_1\,V_0\frac L 2 \,= \frac {m_2\,L^2\,\omega}{12}$$
$$\frac {6m_1V_0} {m_2\,L} = \omega \,\,\,\,\,\,\,\,\,\,. . . (1)$$
##2.##However, If I am to use the fixed point as the origin :
$$m_1\,V_0\, L \,= \frac {m_2\,L^2\,\omega}{3} + m_2V'_2\frac L 2$$
Substituting the Linear momentum equation into this will yields:
$$m_1\,V_0\, L = \frac {m_2\,L^2\,\omega}{3} + m_1V_0\frac L 2$$
$$m_1\,V_0\frac L 2 = \frac {m_2\,L^2\,\omega}{3} $$
$$\frac {3m_1V_0} {2m_2\,L} = \omega \,\,\,\,\,\,\,\,\,\,. . . (2)$$
As you can see, both methods yield different results. Though, it is really unlikely for the book to make a mistake. So, are there any concepts that I did wrong?
##\,\,\,\,\,\,\,\,## "It is important to remember that you are free to choose your origin from the legal possibilities of fixed points or the CM"
Is it really alright to choose the center of a rigid body as an origin even though this body is fixed to a point? because when solving the problem above, I found that both methods yield different result.
Here is my attempt
First, we need to calculate its Linear momentum. (This will be useful when we set the fixed point as an origin)
$$m_1\,V_0\,=\,m_2\,V'_2$$
##1.##Now, If I use the center of the stick as the origin, the angular momentum will be like this :
$$m_1\,V_0\frac L 2 \,= \frac {m_2\,L^2\,\omega}{12}$$
$$\frac {6m_1V_0} {m_2\,L} = \omega \,\,\,\,\,\,\,\,\,\,. . . (1)$$
##2.##However, If I am to use the fixed point as the origin :
$$m_1\,V_0\, L \,= \frac {m_2\,L^2\,\omega}{3} + m_2V'_2\frac L 2$$
Substituting the Linear momentum equation into this will yields:
$$m_1\,V_0\, L = \frac {m_2\,L^2\,\omega}{3} + m_1V_0\frac L 2$$
$$m_1\,V_0\frac L 2 = \frac {m_2\,L^2\,\omega}{3} $$
$$\frac {3m_1V_0} {2m_2\,L} = \omega \,\,\,\,\,\,\,\,\,\,. . . (2)$$
As you can see, both methods yield different results. Though, it is really unlikely for the book to make a mistake. So, are there any concepts that I did wrong?