Confusion on mechanics problem involving cart, blocks, and pulley

[niko_niko]

Homework Statement

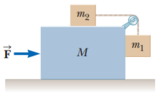
Initially, the system of objects shown in Figure P5.93 (see attached) is held motionless. The pulley and all surfaces and wheels are frictionless. Let the force F be zero and assume that $m_1$ can move only vertically. At the instant after the system of objects is released, find (a) the tension T in the string, (b) the acceleration of $m_2$, (c) the acceleration of M, and (d) the acceleration of $m_1$. (Note: The pulley accelerates along with the cart.)

Relevant Equations

[1] $m_2 (a-A) = T$
[2] $MA = T$
[3] $m_1 a = m_1 g - T$

[Mentor Note -- Two threads on the same by the OP have been merged into one]

I'm having trouble understanding the solution my professor gave me, in particular, the accelerations of m_2 and m_1. When my professor solved for the acceleration of m_2, he used a as the acceleration but when I look at the second law equation for m_2 as shown in eqn. [1], it's a-A. Likewise, when he solved for the acceleration of m_1, he used a-A as the acceleration when according to eqn. [3], it says a. Is this just a simple error on his part or am I misunderstanding something?

 

[niko_niko]

I'm having trouble understanding the solution my professor gave me, in particular, the accelerations of $m_2$ and $m_1$. When my professor solved for the acceleration of $m_2$, he used $a$ as the acceleration but when I look at the second law equation for $m_2$ as shown in eqn. [1], it's $a-A$. Likewise, when he solved for the acceleration of $m_1$, he used $a-A$ as the acceleration when according to eqn. [3], it says $a$. Is this just a simple error on his part or am I misunderstanding something?

 

[haruspex]

Homework Statement: Initially, the system of objects shown in Figure P5.93 (see attached)

Where?

 

[Lnewqban]

Is this the proper figure?

 

[niko_niko]

Where?

Forgot to attach sorry. Here it is.

 

[niko_niko]

Is this the proper figure?

View attachment 329104

Yes, that is also what my professor showed me.

 

[haruspex]

assume that $m_1$ can move only vertically.

I assume that means vertically relative to M.

When my professor solved for the acceleration of $m_2$, he used $a$ as the acceleration but when I look at the second law equation for $m_2$ as shown in eqn. [1], it's $a-A$.

How did your professor define a, as acceleration in the ground frame or relative to M?

 

[niko_niko]

I assume that means vertically relative to M.

How did your professor define a, as acceleration in the ground frame or relative to M?

Well, looking at the second law equations he wrote, I would assume a is measured relative to the ground given that it took into account the acceleration A of the cart. But when he solved for the acceleration of $m_2$ for item (b) he seemed to only use a, as shown in the image below.

 

[haruspex]

Well, looking at the second law equations he wrote, I would assume a is measured relative to the ground given that it took into account the acceleration A of the cart. But when he solved for the acceleration of $m_2$ for item (b) he seemed to only use a, as shown in the image below.

If a is the magnitude of the vertical component of the acceleration of the suspended mass then it is also the acceleration (to the right) of the top mass relative to the block. (Using the constancy of rope length.) If the acceleration of the block is A to the left then the top mass's acceleration to the right in the ground frame is a-A.

 

[niko_niko]

If a is the magnitude of the vertical component of the acceleration of the suspended mass then it is also the acceleration (to the right) of the top mass relative to the block. (Using the constancy of rope length.) If the acceleration of the block is A to the left then the top mass's acceleration to the right in the ground frame is a-A.

So in that case, the solution provided for (b) should be the acceleration for the hanging mass and not the top mass. Am I correct?

 

[haruspex]

So in that case, the solution provided for (b) should be the acceleration for the hanging mass and not the top mass. Am I correct?

No. (b) asks for $m_2$'s acceleration. Since it does not specify relative to the block M, you should take that as acceleration in the ground frame, a-A.

 

[niko_niko]

No. (b) asks for $m_2$'s acceleration. Since it does not specify relative to the block M, you should take that as acceleration in the ground frame, a-A.

But in the solution provided for (b), my professor used a instead of a-A. Likewise, in (d) the acceleration for the hanging mass was a-A according to the solution.

 

[Chestermiller]

Did your professor really write those 3 equations as they are written?

 

[niko_niko]

Did your professor really write those 3 equations as they are written?

Yes. Those are the exact equations that were provided. For reference, I attached the solution my professor gave me containing those equations.

 

[niko_niko]

It seems my question got duplicated. Could the moderators close the other thread: https://www.physicsforums.com/threa...-of-system-of-cart-blocks-and-pulley.1053967/

 

[Chestermiller]

Let $a_B$ represent the acceleration of the large block in the positive x direction, and "a"represent the downward acceleration of m1. Then "a" is also the horizontal acceleration of m2 relative to M, and the absolute horizontal acceleration of m2 is $(a_B+a)$. OK so far?

 

[haruspex]

But in the solution provided for (b), my professor used a instead of a-A. Likewise, in (d) the acceleration for the hanging mass was a-A according to the solution.

First, the solution shows I guessed wrongly about "m₂ only moves vertically". It means that in the ground frame.

Given that, the expression found for $a$ is correct, but it is not the acceleration of the top block in the ground frame.

Looking now at the solution to (d), it seems the solver has become confused between the two masses, as you suspected. The answer to (d) should be the expression found for $a$ and the answer to (b) should be $a-A$.

 

[niko_niko]

Let $a_B$ represent the acceleration of the large block in the positive x direction, and "a"represent the downward acceleration of m1. Then "a" is also the horizontal acceleration of m2 relative to M, and the absolute horizontal acceleration of m2 is $(a_B+a)$. OK so far?

Hmm. Does the large block accelerate in the positive x direction? My assumption is that it should move to the left due to the force exerted by the rope.

 

[Chestermiller]

Hmm. Does the large block accelerate in the positive x direction? My assumption is that it should move to the left due to the force exerted by the rope.

In that case, $a_B$ would come out negative, right? Are you only looking at the case where F = 0?

 

[niko_niko]

In that case, $a_B$ would come out negative, right? Are you only looking at the case where F = 0?

That would be what I would imagine for the case of F=0, yes. Which means the acceleration of the top block should be a-a_B, right?

 

[erobz]

Assume the large block is accelerating to the left with ${}^+\leftarrow$, what do you get for the sum of the forces on that block ( with mass $M$ )?

 

[erobz]

I'm just going to say it. I don't think the solution provided is correct. If $m_1$ can only move in the vertical direction it must be restricted by a track of some sort. That track is essential for providing the force that pulls $m_1$ along in the horizontal direction. As a direct consequence of Newtons 3^rd there is a force that has not been accounted for acting on the large mass $M$ in the solution provided by the prof.

 

[Chestermiller]

I'm just going to say it. I don't think the solution provided is correct. If $m_1$ can only move in the vertical direction it must be restricted by a track of some sort. That track is essential for providing the force that pulls $m_1$ along in the horizontal direction. As a direct consequence of Newtons 3^rd there is a force that has not been accounted for acting on the large mass $M$ in the solution provided by the prof.

If F=0 and the cart is moving to the left, then m1 doesn't contact M.

 

[jbriggs444]

I'm just going to say it. I don't think the solution provided is correct. If $m_1$ can only move in the vertical direction it must be restricted by a track of some sort. That track is essential for providing the force that pulls $m_1$ along in the horizontal direction. As a direct consequence of Newtons 3^rd there is a force that has not been accounted for acting on the large mass $M$ in the solution provided by the prof.

A track is not required. Nor, according to the givens in the problem, can a track (attaching $m_1$ to $M$) be present.

We are only asked for initial forces and accelerations. Initially, the only forces acting on $m_1$ are vertical. Accordingly, the initial acceleration of $m_1$ will be purely vertical. The proviso in the problem statement is not needed.

If, counterfactually, there were a track constraining $m_1$ to follow the face of $M$, then, because $M$ accelerates leftward, so would $m_1$. This would violate the givens of the problem statement which state that $m_1$ moves vertically only.

It would be possible for $m_1$ to be mounted on a vertical guide track anchored to the ground without violating the givens of the problem. This would not "pull $m_1$ along in the horizontal direction" since $m_1$ is stipulated not to move in the horizontal direction. However, since such a track would, at least initially, exert zero force on $m_1$, it would be redundant.

 

[erobz]

We are only asked for initial forces and accelerations. Initially, the only forces acting on $m_1$ are vertical. Accordingly, the initial acceleration of $m_1$ will be purely vertical. The proviso in the problem statement is not needed.

I didn't catch this is to be solved at the instant of release. Skim reading gets me again.

If, counterfactually, there were a track constraining $m_1$ to follow the face of $M$, then, because $M$ accelerates leftward, so would $m_1$. This would violate the givens of the problem statement which state that $m_1$ moves vertically only.

Because of what I was missing above, I figured they meant it only moves vertically in the frame of reference of the cart.

It would be possible for $m_1$ to be mounted on a vertical guide track anchored to the ground without violating the givens of the problem. This would not "pull $m_1$ along in the horizontal direction" since $m_1$ is stipulated not to move in the horizontal direction. However, since such a track would, at least initially, exert zero force on $m_1$, it would be redundant.

Yes, at the instant the restraining forces are released, I agree.

 

[erobz]

If F=0 and the cart is moving to the left, then m1 doesn't contact M.

Sorry, I thought the vertical motion constraint of $m_1$ was w.r.t. the cart. Also, I didn't see we were only to solve at the instant the system is freed.

 

[haruspex]

It seems my question got duplicated. Could the moderators close the other thread: https://www.physicsforums.com/threa...-of-system-of-cart-blocks-and-pulley.1053967/

Rescuing this reply of mine from that other thread:
… the expression found for $a$ is correct, but it is not the acceleration of the top block in the ground frame.

Looking now at the solution to (d), it seems the solver has become confused between the two masses, as you suspected. The answer to (d) should be the expression found for $a$ and the answer to (b) should be $a-A$.

 

[Lnewqban]

...My assumption is that it should move to the left due to the force exerted by the rope.

It is important for you to visualize that is the x-component of T (the magnitude of the angled total force is greater than T), via the pulley and its support, what induces the big block to slide to the left.
The rope itself can only pull m2 and m1.

 

[haruspex]

It is important for you to visualize that is the x-component of T (the magnitude of the angled total force is greater than T), via the pulley and its support, what induces the big block to slide to the left.
The rope itself can only pull m2 and m1.

Seems reasonable to treat the block and pulley as a unit, so @niko_niko is correct to say that the force exerted by the rope causes its acceleration.

 

[niko_niko]

I'm just going to say it. I don't think the solution provided is correct. If $m_1$ can only move in the vertical direction it must be restricted by a track of some sort. That track is essential for providing the force that pulls $m_1$ along in the horizontal direction. As a direct consequence of Newtons 3^rd there is a force that has not been accounted for acting on the large mass $M$ in the solution provided by the prof.

I am convinced that the solution to this problem has to be a mistake for the reason that the accelerations of the top block $m_2$ and the hanging block $m_1$ are simply inconsistent with each other. To reiterate, the solution in item (b) says that the acceleration of the top block is $a$ whereas the solution in item (d) says that the acceleration of the hanging block is $a-A$. There is simply no conceivable way for the vertical acceleration of the hanging block to be $a-A$ if it was stated that the hanging block can only move in the vertical direction.

 

[jbriggs444]

I am convinced that the solution to this problem has to be a mistake for the reason that the accelerations of the top block $m_2$ and the hanging block $m_1$ are simply inconsistent with each other. To reiterate, the solution in item (b) says that the acceleration of the top block is $a$ whereas the solution in item (d) says that the acceleration of the hanging block is $a-A$. There is simply no conceivable way for the vertical acceleration of the hanging block to be $a-A$ if it was stated that the hanging block can only move in the vertical direction.

What reference frame are you adopting when you assert that the horizontal acceleration of $m_2$ is equal to the vertical acceleration of $m_2$?

If you are using the accelerating frame anchored to $M$ then you would be correct. What happens if you shift to the inertial rest frame of the floor? Is the horizontal acceleration of $m_2$ unaffected by the change in reference frame?

 

[niko_niko]

What reference frame are you adopting when you assert that the horizontal acceleration of $m_2$ is equal to the vertical acceleration of $m_2$?

If you are using the accelerating frame anchored to $M$ then you would be correct. What happens if you shift to the inertial rest frame of the floor? Is the horizontal acceleration of $m_2$ unaffected by the change in reference frame?

I shall refer to $m_2$ as the top block for convenience. As for the horizontal acceleration of the top block relative to the ground frame, it should be $a-A$. However, as I have said, the solution says it is simply $a$. As for $m_1$ which I shall refer to as the hanging block, the solution states that it's acceleration is $a-A$, however this can't be the case because the hanging block moves only vertically so the acceleration A of the cart must not be relevant for the case of the hanging block. Please see the solution for (b) and (d), I do not want to post it for the third time.

 

[jbriggs444]

I shall refer to $m_2$ as the top block for convenience. As for the horizontal acceleration of the top block relative to the ground frame, it should be $a-A$. However, as I have said, the solution says it is simply $a$. As for $m_1$ which I shall refer to as the hanging block, the solution states that it's acceleration is $a-A$, however this can't be the case because the hanging block moves only vertically so the acceleration A of the cart must not be relevant for the case of the hanging block. Please see the solution for (b) and (d), I do not want to post it for the third time.

Let me go back and review the proffered solution with which I think you disagree.

So contrary to your assertion $a$ is taken as the vertical acceleration of $m_1$ on the right. Not $m_2$ up top.

$a-A$ is then the horizontal acceleration of $m_2$ up on top. Just as you agree it should be. The pulley is accelerating leftward while block $m_2$ is accelerating rightward.

The rate at which the length of horizontal cord is shortening is given by an acceleration rate of $(a-A) - A = a$. The rate at which the length of vertical cord is lengthening is given by an acceleration rate of $a$. This consistency check passes!

Note that mass $m_1$ will be remaining horizontally in place while mass $M$ moves away to the left. From the point of view of the accelerating rest frame of $M$, mass $m_1$ will be swinging horizontally away.

Are we in agreement so far?

If we examine the equations, we have: $$m_2(a-A) = T$$The acceleration term is relative to the ground frame. We have no inertial pseudo forces to account for. The only horizontal force on $m_2$ is T. So that equation is fine.

We also have: $$m_1a = m_1g - T$$That is, the net downward force on $m_1$ is the downward force from gravity plus the upward force from tension. That seems straightforward enough.

What is your objection?

 

[niko_niko]

Let me go back and review the proffered solution with which I think you disagree.

View attachment 329177

So contrary to your assertion $a$ is taken as the vertical acceleration of $m_1$ on the right. Not $m_2$ up top.

$a-A$ is then the horizontal acceleration of $m_2$ up on top. Just as you agree it should be.

Note that mass $m_1$ will be remaining horizontally in place while mass $M$ moves away to the left. From the point of view of the accelerating rest frame of $M$, mass $m_1$ will be swinging horizontally away.

Are we in agreement so far?

If we examine the equations, we have: $$m_2(a-A) = T$$The acceleration term is relative to the ground frame. We have no inertial pseudo forces to account for. The only horizontal force on $m_2$ is T. So that equation is fine.

We also have: $$m_1a = m_1g - T$$That is the net downward force on $m_1$ is the downward force from gravity plus the upward force from tension. That seems straightforward enough.

What is your objection?

To everything you have stated, I agree. However, my objection does not come from the portion of the solution you have pointed out. Rather, here:

I believe the continued solution here contradicts with the established accelerations in the previous portion of the solution.

 

[jbriggs444]

To everything you have stated, I agree. However, my objection does not come from the portion of the solution you have pointed out. Rather, here:
View attachment 329180
View attachment 329179
I believe the continued solution here contradicts with the established accelerations in the previous portion of the solution.

What I see here is a formula for (b) that evaluates to $a$ which you have agreed is the acceleration of $m_1$. However, (b) was supposed to be about the acceleration of $m_2$.

I suspect that it is a correct answer for (d). Though I have not verified the formula.

What I also see here is a formula for (d) that evaluates to $a-A$ which you have agreed is the acceleration of $m_2$. However, (d) was supposed to be about the acceleration of $m_1$.

I suspect that this is a correct answer for (b). Though I have not verified the formula.