ARoyC
- 56
- 11
Hi. I am not being able to understand how we are getting the following spectral decomposition. It would be great if someone can explain it to me. Thank you in advance.
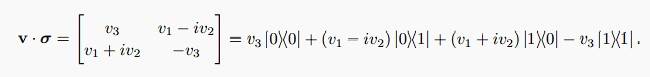
Oh! Then we can go to the LHS of the equation from the RHS. Can't we do the reverse?vanhees71 said:It's simply a non-sensical equation. On the one side you write down a matrix, depicting matrix elements of an operator and on the other the operator itself. Correct is
$$\hat{A}=v_3 |0 \rangle \langle 0| + (v_1-\mathrm{i} v_2) |0 \rangle \langle 1| + (v_1+\mathrm{i} v_2) |1 \rangle \langle 0| - v_3 |1 \rangle \langle 1|.$$
The matrix elements in your matrix are then taken with respect to the basis ##(|0 \rangle,|1 \rangle)##.
$$(A_{jk})=\langle j|\hat{A}|k \rangle, \quad j,k \in \{0,1 \}.$$
To see this, simply use ##\langle j|k \rangle=\delta_{jk}##. Then you get, e.g.,
$$A_{01}=\langle 0|\hat{A}|1 \rangle=v_1-\mathrm{i} v_2.$$
How are we getting the very first equality that is A = Σ|j><j|A|k><k| ?vanhees71 said:Sure:
$$\hat{A}=\sum_{j,k} |j \rangle \langle j|\hat{A}|k \rangle \langle k| = \sum_{jk} A_{jk} |j \rangle \langle k|.$$
The mapping from operators to matrix elements with respect to a complete orthonormal system is one-to-one. As very many formal manipulations in QT, it's just using the completeness relation,
$$\sum_j |j \rangle \langle j|=\hat{1}.$$
Oh, okay, thanks a lot!Haborix said:$$\hat{A}=\hat{1}\hat{A}\hat{1}=\left(\sum_{j} |j \rangle \langle j|\right)\hat{A}\left(\sum_{k} |k \rangle \langle k|\right)=\sum_{j,k} |j \rangle \langle j|\hat{A}|k \rangle \langle k| = \sum_{jk} A_{jk} |j \rangle \langle k|.$$