Confusion when considering pV=nRT in Two Balloon experiment

[phantomvommand]

This is the Two-Balloon Experiment: https://en.wikipedia.org/wiki/Two-balloon_experiment#cite_note-MW78-1

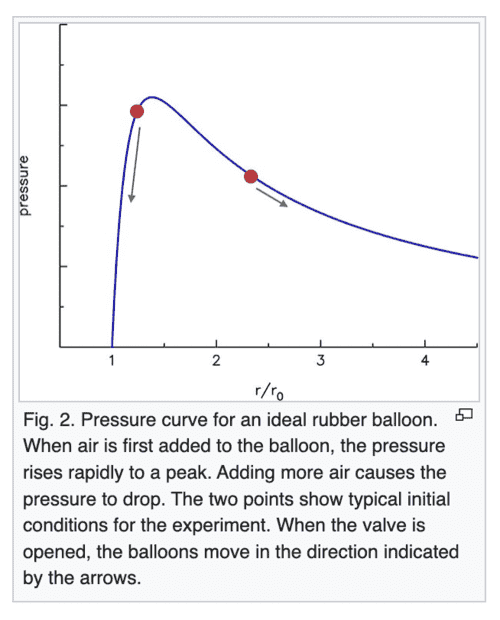
The claim on Wikipedia which I am a little confused over is that when 2 balloons (at the 2 red points) are connected via a tube, the smaller balloon at a higher pressure would push air into the larger balloon. Eventually, the pressure should become equal in both balloons.

My first question is this:
According to the article, the "pressure" that must become equal eventually is the pressure in the rubber of the balloon. However, shouldn't it be the pressure of the air in the 2 balloons?

Assuming that equal rubber pressure implies equal air pressure,
considering the system as a whole:
P1V1 + P2V2 must be equal to P(V1 + V2), where P is the final equal air pressure. However, P1 > P and P2 > P, so the equality cannot hold. (LHS > RHS)

I understand that I have not accounted for the changes in energy when the rubber balloons acquire a more stable state (at lower pressure). But if this were accounted for, we can see that:
U1 + U2 + Rubber energy initial = U3 + Rubber energy final, where U1, U2, and U3 are the internal energies of the air in the small balloon, bigger balloon and final state.
Since U1, U2, U3 are analogous to P1V1, P1V2, and P(V1+V2), and rubber energy final > initial, LHS > RHS.

Where have I gone wrong?

 

[Baluncore]

However, shouldn't it be the pressure of the air in the 2 balloons?

True. Once the two balloons have equilibrated, there is only one volume, so the air pressure in the two balloons must be equal. The radii of the balloons will be different, as will be the tension in the rubber.

Assuming that equal rubber pressure implies equal air pressure, considering the system as a whole:

That is a false assumption.
The balloon radius of curvature relates the air pressure to the tension in the rubber material.

 

[phantomvommand]

The radii of the balloons will be different, as will be the tension in the rubber.

However, the wiki article seems to suggest that the final tension in the rubber will become equal.
<The air flow ceases when the two balloons have equal pressure, with one on the left branch of the pressure curve (r<rp) and one on the right branch (r>rp)>

rp refers to the peak rubber pressure in my original post.

 

[Baluncore]

<The air flow ceases when the two balloons have equal pressure, with one on the left branch of the pressure curve (r<rp) and one on the right branch (r>rp)>

The surface tension in the rubber balloon opposes the difference between internal and external air pressure. The rubber membrane has no pressure, it has tension.
Surface tension in the rubber, is perpendicular to the differential air pressure.

 

[phantomvommand]

The surface tension in the rubber balloon opposes the difference between internal and external air pressure. The rubber membrane has no pressure, it has tension.
Surface tension in the rubber, is perpendicular to the differential air pressure.

So the graph is actually the pressure of air in the balloon as it expands?

However, explanations online all claim that the graph represents the tension in the rubber...

And if it is the pressure of air in the balloon, then:
considering the system as a whole:
P1V1 + P2V2 must be equal to P(V1 + V2), where P is the final equal air pressure. However, P1 > P and P2 > P, so the equality cannot hold. (LHS > RHS)

 

[Baluncore]

P1V1 + P2V2 must be equal to P(V1 + V2), ...

I do not think so.
The final volume is V, not (V1 + V2). V will be greater than (V1 + V2), since high pressure air from the smaller balloon will expand as it migrates to the larger, lower pressure balloon.

 

[phantomvommand]

I do not think so.
The final volume is V, not (V1 + V2). V will be greater than (V1 + V2), since high pressure air from the smaller balloon will expand as it migrates to the larger, lower pressure balloon.

Thanks for this.

Would my interpretation of the graph as follows be correct:

- the graph actually depicts the air pressure in the balloon.
- the explanation of the air pressure is due to the material properties of rubber (stiff at first — where the increase in number of moles of air leads to P being the main variable increased, but then at some point when rubber expands more easily, V accounts for the main increase in nRT, while P in fact decreases but PV as a whole increases)

 

[Baluncore]

- the graph actually depicts the air pressure in the balloon.

Correct. The pressure is plotted against the relative radius of the balloon.

The explanation should include the changing thickness, and the radius of curvature of the membrane.