- #1
Spencer25
- 13
- 4
- Homework Statement
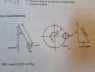
- A 3m long string is attached to a 5kg mass and rotates at 5 rpm. Calculate the height of the pendulum.
- Relevant Equations
- H=g/w2 (Height = gravity divided by angular velocity squared)
= 9.81/ .27415 = 35.78m
So in this instance height is longer than the 3m string which is impossible. Do we just say that when ever H>L, H=L?