Conservation of energy problem: Ball rolling down inclined plane and then through a loop-the-loop

[SiRiVeon]

Homework Statement

What is the minimum height of the triangle for which if the black ball falls through the inclined
plane, it will be able to make a full cycle around the circle at the bottom of the inclined plane of
radius R?

Relevant Equations

mgh = (1/2)mv² + (1/2)Iω² , = (2/5)mr² , v = ωr , Centripetal force = mv²/r

Hello, this question may seem weird but I really need help on this.

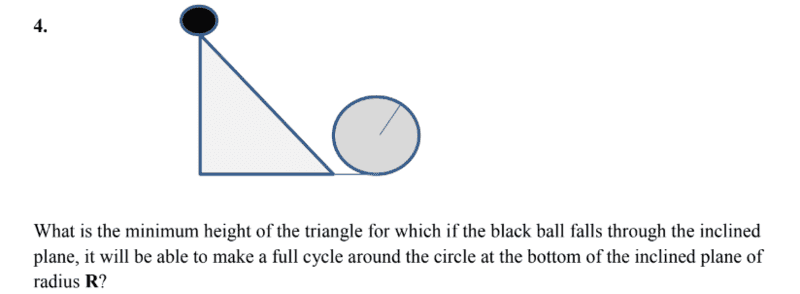
To bring the formula for the height h of the triangle above, I have to create a relation between potential and kinetic energies of the black ball with mass m (I can't find any other methods than this).
For a sphere falling through an inclined plane, the equation to satisfy it's conservation of energy is mgh = (1/2)mv² + (1/2)Iω² where v is the linear velocity of the ball, g is the acceleration due to gravity, ω is the rotational velocity of the ball and I is the moment of inertia of the ball which can be expressed by I = kmr² where k = 2/5 for sphere of radius r. By putting ω = v/r and expression of I into the first equation, I get mgh = (1/2)mv² + (1/5)mv² .
But in the given question, it says that the ball makes a full cycle around the circle of radius R at the bottom of the inclined plane. So what should be the conservation of energy in this case? If the centripetal force to move around that circle is mv²/R then will it be mgh = (1/2)mv² + (1/5)mv² + mv²/R for the whole scenario or will it be mv²/R = (1/2)mv² + (1/5)mv² or none of this?

 

[anuttarasammyak]

Hmm... it seems unnatural that black ball go round the R circle after it falls down. Radius of black ball, say r, is allowed to have any value ? For r>R, h>2R seems reasonable.

 

[SiRiVeon]

Hmm... it seems unnatural that black ball go round the R circle after it falls down. Radius of black ball, say r, is allowed to have any value ? For r>R, h>2R seems reasonable.

There's no radius mentioned for the black ball so I assumed it has a radius r. Radius r can be allowed to have value but I was hoping if it can be solved without any complexities of ball radius. I just need to know what the height of the triangle needs to be, if it can be solved other than conservation of energy way than that's fine too

 

[haruspex]

There's no radius mentioned for the black ball so I assumed it has a radius r.

I would assume its radius is negligible compared to R.
Consider the forces acting at the top of the circle.

 

[SiRiVeon]

I would assume its radius is negligible compared to R.
Consider the forces acting at the top of the circle.

Okay. I think the circle is more like a Diavolo loop where Newton's law gives us -Fₙ -Fg = m(-v²/R) or mv²/R = mg. Solving this I get v = √(gR) which is the minimum velocity needed to move around the loop. By putting the equation of v into mgh = (1/2)mv² + (1/5)mv² and solving it, the height I found out is h = 7R/10. Is this correct?

 

[kuruman]

Is this correct?

Two reasons why it is not correct.

You measure potential energy from the bottom of th loop and you start with initial mechanical energy (kinetic + potential) $ME_i=mgh$. When the ball reaches the top of the loop it has potential energy $U_g=mg(2R)$ which you omitted from your expression of mechanical energy conservation.

You assume that the ball has zero radius for purposes of potential energy and centripetal acceleration. However, under that assumption, the moment of inertia $I=kmr^2$ must be zero. You cannot have it both ways. You should rewrite the equations considering that the center of mass of the ball is at distance $R-r$ from the center of the loop.

Usually this problem is solved by assuming a point mass that does not roll as @haruspex suggested in post #4. If the ball rolls without slipping, that piece of information is explicitly mentioned in the statement of the problem.

 

[SiRiVeon]

Two reasons why it is not correct.

You measure potential energy from the bottom of th loop and you start with initial mechanical energy (kinetic + potential) $ME_i=mgh$. When the ball reaches the top of the loop it has potential energy $U_g=mg(2R)$ which you omitted from your expression of mechanical energy conservation.

You assume that the ball has zero radius for purposes of potential energy and centripetal acceleration. However, under that assumption, the moment of inertia $I=kmr^2$ must be zero. You cannot have it both ways. You should rewrite the equations considering that the center of mass of the ball is at distance $R-r$ from the center of the loop.

Usually this problem is solved by assuming a point mass that does not roll as @haruspex suggested in post #4. If the ball rolls without slipping, that piece of information is explicitly mentioned in the statement of the problem.

Thank you sir. So if I consider the ball as a point mass then before touching the bottom of the slope, the conservation of energy of the ball will be mgh = (1/2)mv² and since it has to pass the loop with that energy, the equation will be mgh = (1/2)mv² = mg(2R). Therefore by solving, the height h of the triangle should be 2R or am I still doing wrong?

 

[erobz]

Thank you sir. So if I consider the ball as a point mass then before touching the bottom of the slope, the conservation of energy of the ball will be mgh = (1/2)mv² and since it has to pass the loop with that energy, the equation will be mgh = (1/2)mv² = mg(2R). Therefore by solving, the height h of the triangle should be 2R or am I still doing wrong?

You’ve done it wrong. It has kinetic energy AND potential energy at the top of the loop.

 

[kuruman]

Thank you sir. So if I consider the ball as a point mass then before touching the bottom of the slope, the conservation of energy of the ball will be mgh = (1/2)mv² and since it has to pass the loop with that energy, the equation will be mgh = (1/2)mv² = mg(2R). Therefore by solving, the height h of the triangle should be 2R or am I still doing wrong?

Mechanical energy conservation says that kinetic plus potential energy at some point A is the same as kinetic plus potential energy at another point B. In some problems one or the other (or both) could be zero at one point but this does not mean that one or the other MUST be zero at a given point.

 

[haruspex]

You assume that the ball has zero radius for purposes of potential energy and centripetal acceleration. However, under that assumption, the moment of inertia $I=kmr^2$ must be zero. You cannot have it both ways.

Indeed you can, and should.
Zero radius is an idealisation, so should be treated as the limit of real scenarios. If we solve the problem for a nonzero radius r then take the limit, its effect in changing the height of the mass centre vanishes, but the fraction of KE in rotational energy is constant.

 

[kuruman]

Indeed you can, and should.
Zero radius is an idealisation, so should be treated as the limit of real scenarios. If we solve the problem for a nonzero radius r then take the limit, its effect in changing the height of the mass centre vanishes, but the fraction of KE in rotational energy is constant.

Yes, I posted without thinking.