heroslayer99
- 33
- 6
- Homework Statement
- A particle of mass m is suspended from a fixed point O by a light spring of natural length a and modulus of elasticity 4mg, the particle is pulled vertically down a distance d from its equilibrium position and released, find d if the particle just reaches O.
- Relevant Equations
- T = modulus of elasticity (extension) / natural length
EPE = modulus of elasticity (extension)^2 / 2 x natural length
Start by finding the equilibrium position, so we have {4mgx}/{a} = mg giving us x = a/4, therefore the spring's length is 5a/4. Now the loss in EPE (and therefore gain in energy of the particle) between the bottom and the equilibrium position is clearly 4mg((a/4 + d)^2 , and then from the equilibrium position up to O, the particle loses 4mg(a^2)/2a (as this is the gain in EPE), therefore in total the particle's energy has changed by 4mg((a/4 + d)^2 - 4mg(a^2)/2a, and this should equal the change in GPE (- the work done by gravity), which is clearly mg(5a/4 + d), this gives us d=5/4(a), whereas my textbook does something else, could someone let me know if either mine or the textbook's working is wrong? Thanks
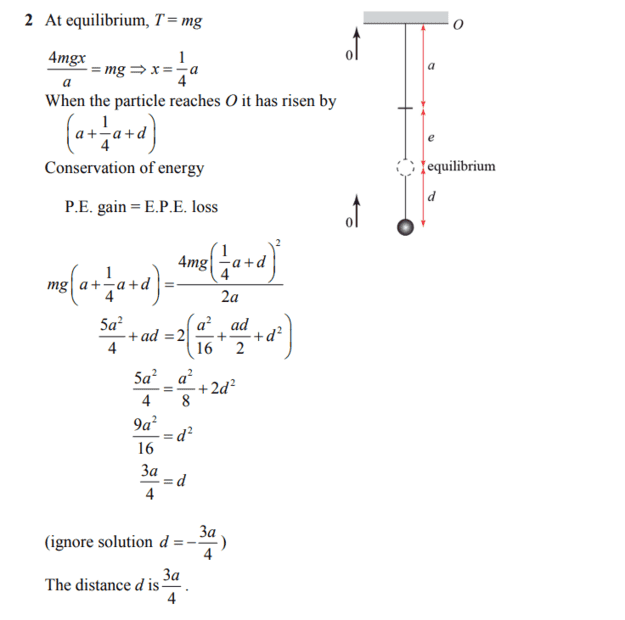
Last edited: