Conservation of relativistic energy, collision of particles

[milkism]

Homework Statement

Collision of a proton and antiproton forming bunch of pions, what's the maximum amount?

Relevant Equations

$$E=\gamma mc^2$$

Question:

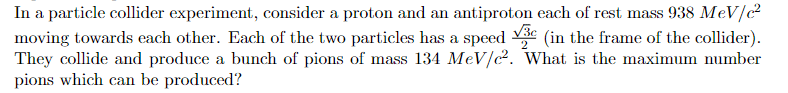
With maximum do they mean that the speed of the pions is the same as the proton and an antiproton? Otherwise there will be two unknowns, and if I use both relativistic-energy and momentum conservation equations I get difficult equations.

 

[Doc Al]

With maximum do they mean that the speed of the pions is the same as the proton and an antiproton?

No reason to think that. To find the maximum number of pions, what might you assume about their speeds?

 

[milkism]

No reason to think that. To find the maximum number of pions, what might you assume about their speeds?

I have no idea ,I'm sorry.

 

[Doc Al]

What's the total momentum of the system?

 

[milkism]

Zero.

 

[Doc Al]

Right! So how about assuming that all the created pions have zero momentum -- all the energy goes into their rest masses.

 

[milkism]

What's the total momentum of the

Right! So how about assuming that all the created pions have zero momentum -- all the energy goes into their rest masses.

Wouldn't that be $$E=nmc^2$$, with n amount.

 

[Doc Al]

You're given the rest mass of the pions. How much total energy does the system have to create particles with?

 

[milkism]

You're given the rest mass of the pions. How much total energy does the system have to create particles with?

3752 MeV?

 

[Ibix]

3752 MeV?

You should at least sketch out why you think that. You're right, but you may have made two cancelling mistakes.

So how many pions can you get from that?

 

[milkism]

You should at least sketch out why you think that. You're right, but you may have made two cancelling mistakes.

So how many pions can you get from that?

Using $$E=\gamma mc^2$$, calculating the Lorentz factor with the given velocity will be 2, so E becomes 2mc², but because both proton and antiproton have same mass and velocity, the total energy will be 4mc², that's how I got 3752 MeV.
So we have 3752 = nmc² = > 3752 MeV= n *134 MeV => 28 pions.
If the pions had the same velocity as the proton and antiproton it would have be 14 pions, that's what I had at first.

 

[Ibix]

Right.

Note that they've fudged the numbers so it comes out nice and round. The neutral pion mass is nearly 135MeV, while protons are only a bit over 938MeV. You'd need to speed your protons up a bit more to have enough energy for 28 pions.

 

[Doc Al]

So we have 3752 = nmc² = > 3752 MeV= n *134 MeV => 28 pions.

Good! (Thanks for jumping in, @Ibix -- I got called away.)

 

[Ibix]

Thanks for jumping in, @Ibix -- I got called away.

Thanks for not saying "butting in".

 

[kuruman]

What's the total momentum of the system?

Of course, the proton-antiproton pair must be spin-coupled in the singlet state to conserve angular momentum as well. That might be a bit tricky to achieve in a particle collider.

 

[Doc Al]

Of course, the proton-antiproton pair must be spin-coupled in the singlet state to conserve angular momentum as well. That might be a bit tricky to achieve in a particle collider.

Indeed. For the purpose of this exercise I think those worries can be ignored.