mancity
- 26
- 2
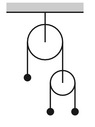
- Homework Statement
- Explain why the acceleration of the left mass equals negative the average of the accelerations of the right two masses.
- Relevant Equations
- Conservation of string
I'm not quite sure how to apply conservation of string to this problem, so guidance would be appreciated. Normally as long as there isn't a "sub-pulley" I can do the problem fairly easily but this one tricks me up. Thanks