Conserved quantities via Poisson brackets

[Lambda96]

Homework Statement

Show that $L_j^{(1)}+L_j^{(2)}$ is preserved

Relevant Equations

See screenshot

Hi,

Results from the previous task, which we may use

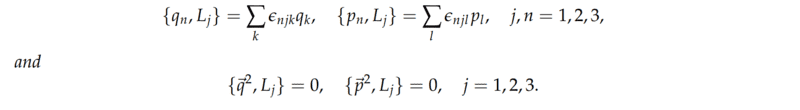I am unfortunately stuck with the following task

Hi,

I have first started to rewrite the Hamiltonian and the angular momentum from vector notation to scalar notation:

$$H=\frac{1}{2m}\vec{p_1}^2+\frac{1}{2m}\vec{p_2}^2-\alpha|\vec{q_1}- \vec{q_2}|^2= \sum\limits_{i=1}^{3}\frac{1}{2m}p_{1i}^2+ \sum\limits_{i=1}^{3}\frac{1}{2m}p_{2i}^2-\alpha \sum\limits_{i=1}^{3}(q_{1i}-q_{2i})^2$$

$$L_j^{(1)}+L_j^{(2)}=\sum\limits_{k,l}\epsilon_{jkl}q_k^{(1)}p_l^{(1)}+\sum\limits_{k,l}\epsilon_{jkl}q_k^{(2)}p_l^{(2)}$$

Before inserting the above values into the Poisson bracket, I have rewritten the Poisson bracket as follows

$$\{ H,L_j^{(1)}+L_j^{(2)} \}=\{ H,L_j^{(1)}\}+\{H,L_j^{(2)} \}$$

To save paperwork, I will now only calculate $\{ H,L_j^{(1)}\}$. the calculation for $L_j^{(2)$ would run analogously

$$\{ \sum\limits_{i=1}^{3}\frac{1}{2m}p_{1i}^2+ \sum\limits_{i=1}^{3}\frac{1}{2m}p_{2i}^2-\alpha \sum\limits_{i=1}^{3}(q_{1i}-q_{2i})^2, \sum\limits_{k,l}\epsilon_{jkl}q_k^{(1)}p_l^{(1)}\}$$
$$\{ \sum\limits_{i=1}^{3}\frac{1}{2m}p_{1i}^2,\sum\limits_{k,l}\epsilon_{jkl}q_k^{(1)}p_l^{(1)}\}+ \{\sum\limits_{i=1}^{3}\frac{1}{2m}p_{2i}^2,\sum\limits_{k,l}\epsilon_{jkl}q_k^{(1)}p_l^{(1)}\}+ \{-\alpha \sum\limits_{i=1}^{3}(q_{1i}-q_{2i})^2, \sum\limits_{k,l}\epsilon_{jkl}q_k^{(1)}p_l^{(1)}\}$$

 

[Lambda96]

Because of the previous problem, the terms with $q^2$ become zero, so $\{ \vec{q}^2,L_j \}=0$ also the terms with the different variables become zero and only the following term remains

$$\{-\alpha \sum\limits_{i=1}^{3}(q_{1i}-q_{2i})^2, \sum\limits_{k,l}\epsilon_{jkl}q_k^{(1)}p_l^{(1)}\}$$

Now you can square the bracket off and get $q^2$ terms again, which again add up to zero, leaving only the following term.

$$\{\alpha \sum\limits_{i=1}^{3}q_{1i}q_{2i}, \sum\limits_{k,l}\epsilon_{jkl}q_k^{(1)}p_l^{(1)}\}$$

For the left-hand side I have now used Leibniz's rule and the following applies to the term then $\{q_{2i},q_k^{(1)}p_l^{(1)} \}=0$ and the following term remains

$$\{\alpha \sum\limits_{i=1}^{3}q_{1i}, \sum\limits_{k,l}\epsilon_{jkl}q_k^{(1)}p_l^{(1)}\}q_{2i}$$

Now you can factor out some terms and get the following representation

$$\alpha \sum\limits_{i=1}^{3}\sum\limits_{k,l}\epsilon_{jkl}\{q_{1i}, q_k^{(1)}p_l^{(1)}\}q_{2i}$$

Now you can use the result from the previous task and get

$$\epsilon_{jki}q_k^{(1)}q_i^{(2)}$$

for the calculation $\{H,L_j^{(2)} \}$ I got the following $\epsilon_{jki}q_k^{(2)}q_i^{(1)}$, so I get as final result:

$$\epsilon_{jki}q_k^{(1)}q_i^{(2)}+\epsilon_{jki}q_k^{(2)}q_i^{(1)}$$

Actually, the result should be 0 in order to conserve the observable, have I miscalculated somewhere or can I still zero the above term with an index manipulation?

Sorry to split my calculation into two posts, but when I do the whole calculation in one post, it is not displayed correctly.

 

[TSny]

so I get as final result:
$$\epsilon_{jki}q_k^{(1)}q_i^{(2)}+\epsilon_{jki}q_k^{(2)}q_i^{(1)}$$
Actually, the result should be 0

I think you are essentially there. Play with the expression above and see if you can see why it equals 0. Note that $k$ and $i$ are dummy summation indices.

 

[Lambda96]

Thank you for your help TSny

I have now proceeded as follows

$$\epsilon_{jki}q_k^{(1)}q_i^{(2)}+\epsilon_{jki}q_k^{(2)}q_i^{(1)}$$

Now in the second term I have swapped the indices of $q_k^{(2)}q_i^{(1)}$ to $q_i^{(2)}q_k^{(1)}$.

$$\epsilon_{jki}q_k^{(1)}q_i^{(2)}+\epsilon_{jik}q_i^{(2)}q_k^{(1)}$$

By doing this, I have made an anticyclic permutation to the Levi-Civita symbol, which makes it negative and I can write the above equation as follows.

$$\epsilon_{jki}q_k^{(1)}q_i^{(2)}-\epsilon_{jik}q_i^{(2)}q_j^{(1)}=0$$

 

[TSny]

I have now proceeded as follows

$$\epsilon_{jki}q_k^{(1)}q_i^{(2)}+\epsilon_{jki}q_k^{(2)}q_i^{(1)}$$

Now in the second term I have swapped the indices of $q_k^{(2)}q_i^{(1)}$ to $q_i^{(2)}q_k^{(1)}$.

$$\epsilon_{jki}q_k^{(1)}q_i^{(2)}+\epsilon_{jik}q_i^{(2)}q_k^{(1)}$$

This looks good. Note that the index $j$ is a fixed index that is not summed. It corresponds to the fixed index $j$ that you started with in the expression $\{H, L_j^{(1)}\}$. The reason that you were allowed to swap the indices $i$ and $k$ in the second term is that you are summing over $i$ and $k$. That is, the equality $$\epsilon_{jki}q_k^{(1)}q_i^{(2)} + \epsilon_{jki}q_k^{(2)}q_i^{(1)} =\epsilon_{jki}q_k^{(1)}q_i^{(2)} + \epsilon_{jik}q_i^{(2)}q_k^{(1)}$$ should actually be written as $$\sum_{k, i}\left(\epsilon_{jki}q_k^{(1)}q_i^{(2)} + \epsilon_{jki}q_k^{(2)}q_i^{(1)} \right) =\sum_{k, i}\left(\epsilon_{jki}q_k^{(1)}q_i^{(2)} + \epsilon_{jik}q_i^{(2)}q_k^{(1)}\right)$$ It's only because of the summation over $i$ and $k$ that we have equality of these two expressions.

Let me know if this is not clear.

By doing this, I have made an anticyclic permutation to the Levi-Civita symbol, which makes it negative and I can write the above equation as follows.

$$\epsilon_{jki}q_k^{(1)}q_i^{(2)}-\epsilon_{jik}q_i^{(2)}q_j^{(1)}=0$$

The second term is not correct. Double-check this term to make sure this is what you intended to type. The index $j$ should still be a fixed index that occurs only in the levi-civita symbol and a summation over $k$ and $i$ should be included.

 

[Lambda96]

Thank you for your help and explanation TSny

In my notes I had included the sum over k and had unfortunately forgotten to include this in my post 4, but in my notes I had forgotten the sum over i in the course of the calculation, thanks to your explanation I have now noticed this, thank you very much.

Unfortunately I can't quite understand why I wrote j instead of k in my last equation, probably I just did too much index notation the last couple of days

Thanks again for your help

 

[vanhees71]

One can also argue without any calculation ;-)). The total angular momentum $\vec{J}=\vec{L}^{(1)}+\vec{L}^{(2)}$ generate rotations for all vector quantities of both systems, from this you get that $\vec{V}^{(j)} \cdot \vec{W}^{(k)}$ as scalars commute with all components of $\vec{J}$.