Constant Charge/Current Densities with Accelerating Charges

[particlezoo]

In classical physics, when electric charges accelerate, they are expected to radiate. Electromagnetic waves, are by their nature the result of changing electric and magnetic fields. But is it possible to have acceleration of charges without having changing electric and magnetic fields?

One thought that comes to mind (but with changing charge densities) is when charges on a conductor are transferred to a rubber conveyor belt, like in a Van de Graff Generator:

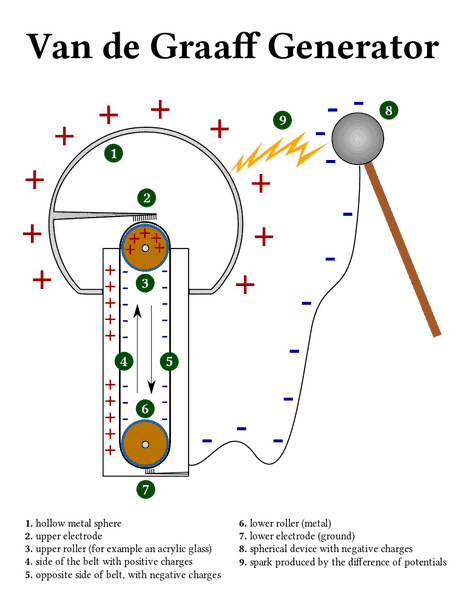
In this case we have charges being transported via a conveyor belt where they travel much faster than the drift velocity in the conducting wire. Therefore, charges must accelerate when the go onto the conveyor belt and "decelerate" when they go off the conveyor belt. Charge density in this case is not constant but accumulated in one region at the expense of another.

But what if we had a c-shaped conductive conveyor belt that pulled a constant current off one end of a conductive wire, only to transfer those charges back onto the other end of the conductive wire?

⊂⊃

We would have two small regions where the charges would be accelerated, but the charge densities and current densities in this case are constant. This is due to convective acceleration (as distinct from local/Eulerian acceleration). From http://web.mit.edu/fluids-modules/www/potential_flows/LecturesHTML/lec02/lecture2.html:
http://web.mit.edu/fluids-modules/www/potential_flows/LecturesHTML/lec02/img37.gif
In this case, would: 1) the electric field in these regions look like that of a constant current (i.e. no curl of the electric field), or 2) would a curl of the electric field show up? Note that the acceleration of charges in each region is unidirectional, so we would not expect the emitted electric field to look like that of an oscillating charge. However, doesn't the acceleration of charge in these regions mean that there should be a transverse electric field distortion?

In the image below (from http://www.tapir.caltech.edu/~teviet/Waves/empulse.html) we have a charge subject to an impulse of a finite time duration. The result is a component of the electric field that is transverse.

If we have charges in a current jumping from one conductor to another conductor in relative motion (such as in a slip ring), then we should expect that these charges will be accelerating. But in our case this acceleration occurs in a "pillbox" that is moving inertially (if moving at all). So if we imagine a steady flow of electrons between these conductors, we should expect a curl of the electric field be produced due to the individual acceleration of each electron. We would in effect have an electric field that could induce current in a separate wire loop. But if that is true, then the only time we might expect the transverse distortion of the electric field to reverse is if we were to reverse the current. So this induction in question would not be alternating, as if being produced by an ever-increasing magnetic field (which clearly ISN'T happening here). A steady direct current could easily be supplied by a battery, and such current crossing the gaps between two relatively moving conductors would consist of accelerating charges, and so CLEARLY we have a problem.

The Maxwell-Faraday equation (one of Maxwell's equations - see above) says that the curl of an electric field occurs simultaneously with a changing magnetic field, but here the current densities are constant and so our magnetic fields should also be constant (despite acceleration of charge across the gaps between the two relatively moving conductors). If the curl of the electric field is non-vanishing in these conditions due to the convective acceleration of charges, then it would violate the Maxwell-Faraday equation. But then, if we were to enforce the Maxwell-Faraday equation, then that is to say that despite the acceleration of charges, the induced electric field would be curl free. Why wouldn't the accelerating charges in the gaps induce an emf in a external conductive loop? Or would they actually do so without changing magnetic fields (which would violate the Maxwell-Faraday equation)?

Also another thing to note is:

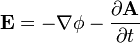
Taking this as the definition of the electric field, will the last term be non-zero due to the convective acceleration of charges in the gaps, or will it be zero due to constant nature of the current densities?

Any clarification is much welcome.

- Kevin M.

 

[Dale]

We would have two small regions where the charges would be accelerated, but the charge densities and current densities in this case are constant. ... However, doesn't the acceleration of charge in these regions mean that there should be a transverse electric field distortion?

You are forgetting about the charge carriers that decelerate. Since the current density is constant for every charge carrier that accelerates there is also one that decelerates to wait for its turn. That field cancels out the other one.

Edit: hold on, this may be incorrect.

 

[particlezoo]

You are forgetting about the charge carriers that decelerate. Since the current density is constant for every charge carrier that accelerates there is also one that decelerates. That field cancels out the other one.

Acceleration has units of m/s^2. But forces have units of kg m/s^2. Since the electrons repel electrons which also attract protons, then the protons would also bear the forces due to electrons being accelerated, not just other electrons. So there is no reason for the acceleration of the electrons to be equal and opposite.

 

[Dale]

I wasn't thinking of forces at all, but I realized that the way I was thinking was incorrect.

So, for the charge carriers to have a higher velocity and the same current density that means that the charge density is lower. Since $J=\rho v$ if $J$ is constant and $v$ increases then $\rho$ decreases.

So we expect an E field anyway.

 

[particlezoo]

I wasn't thinking of forces at all, but I realized that the way I was thinking was incorrect.

So, for the charge carriers to have a higher velocity and the same current density that means that the charge density is lower. Since $J=\rho v$ if $J$ is constant and $v$ increases then $\rho$ decreases.

So we expect an E field anyway.

Okay.

Now something that bothers me is what this would mean for the following:

I am trying to understand what results from this. If we are talking about the transverse electric field, then the first term cannot explain that as it is simply the negative gradient of a scalar field. Only the second term would originate the transverse electric field. However, if we have constant current densities, it is hard to imagine how this could possibly maintain the same rate of change. Something does not seem right about this to me.

 

[Dale]

If we are talking about the transverse electric field, then the first term cannot explain that as it is simply the negative gradient of a scalar field. Only the second term would originate the transverse electric field.

I am not sure what you mean by "transverse" in this context, but in the Lorenz gauge you can just apply Jefimenko's equations to see that A is constant so that term is 0. The E field would be entirely due to the charge density and would indeed be the negative gradient of a scalar field.

If you are thinking of some different field then you are making a mistake.

 

[particlezoo]

I am not sure what you mean by "transverse" in this context

By "transverse", I meant the rotational part of the field.

but in the Lorenz gauge you can just apply Jefimenko's equations to see that A is constant so that term is 0. The E field would be entirely due to the charge density and would indeed be the negative gradient of a scalar field.

If you are thinking of some different field then you are making a mistake.

So even though the electrons would be accelerating, in this case since the charge and current densities are constant, what you are basically saying here is that the E-field is still non-rotational.

 

[Vanadium 50]

Do you have a changing multipole? If you don't, there's no radiation.

 

[particlezoo]

Do you have a changing multipole?

No. In my example, the electrons are accelerating, but the charge and current density distributions are constant. If I imagine the rotational part of the electric field of each charge, only the elements or "pill boxes" bearing the accelerating charges would be contributing to the curl of the electric field. If these elements are stationary (as might be the case between a carbon brush and a rotating slip ring), then this rotational part of the electric field would be "static" in the sense that it would be constant in time, and would not resemble at all any sort of electromagnetic radiation. However, my concern has been that this would be at odds with one of Maxwell's laws (i.e. the Maxwell-Faraday equation) which requires that a rotational electric field co-exist with a changing magnetic field, which requires a changing magnetic vector potential. DaleSpam has essentially answered that because the vector potential is constant, then the rotational part of the electric field does not show up, as required by that law. But then it is hard to square this with the view that the electric field of each charge should add up linearly, including the rotational part of the electric field due to the (convectively) accelerating charges, as electric fields are supposed to obey the principle of superposition.

 

[jartsa]

Well, if a conveyor belt is made of tungsten and it has a high velocity relative to electrons, then X-rays are produced when the electrons and the belt meet.

Slower speed, softer radiation, I guess.

How about a superconducting wire with one thicker part? Well, the speed of electrons is such that high energy photons can't be produced in any collision, and the electrons collide on a soft barrier when they slow down when arriving at the thick part. So just very small amount of very low frequency radiation in this case.

 

[Dale]

By "transverse", I meant the rotational part of the field

In your described setup there is none.

So even though the electrons would be accelerating, in this case since the charge and current densities are constant, what you are basically saying here is that the E-field is still non-rotational

Yes. That follows directly from the retarded potentials.

 

[Vanadium 50]

No. In my example, the electrons are accelerating, but the charge and current density distributions are constant.

Then you don't have radiation.

 

[Dale]

But then it is hard to square this with the view that the electric field of each charge should add up linearly, including the rotational part of the electric field due to the (convectively) accelerating charges, as electric fields are supposed to obey the principle of superposition

The problem is that you didn't really apply the principle of superposition. To apply the principle of superposition you have to first, break the source up into several easy pieces. Then you have to find the fields from each piece. Then you have to add the fields together.

You implicitly broke the source up into a bunch of point charges. But then you only calculated the field from one. And because you only calculated the field from one you didn't have anything to add together.

I have not done the calculation for this specific scenario, but from first principles and from working other similar problems I can guarantee you that if you actually apply the principle of superposition correctly then you will get the same answer as with the retarded potentials.

 

[Dale]

Btw, an easier problem which may be more tractable is to use the retarded potentials and superposition to determine the fields at the center of a rotating ring of charge. This is simplified geometry, but still has the property that each individual charge is accelerating but the overall charge and current distributions are static.