Constraint equation for a solid disk

[Niner49er52]

Homework Statement

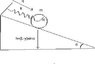
I'm wondering how to write the equation of constraint for a solid disk (mass m, radius R) that is attached to a spring (spring constant k) and rolls without slipping. Any suggestions?

Homework Equations

there are no equations to use, but this has to do with lagrange's equations of motion

The Attempt at a Solution

my first thought was to set this equal to the arclength, but realized that wouldn't work as it is attached to a spring. I am just unsure of how to incorporate the spring into the equation

 

[gabbagabbahey]

The first step is to choose an appropriate coordinate system...I can think of at least two reasonable choices for the origin..how about you?

The next step is to analyze what happens to a point on the disk as it rolls...I would look at the point where the spring is connected...what happens to this point?

 

[Niner49er52]

lets choose the y-direction to be the way in which it is rolling. the disk is rolling about that point

 

[gabbagabbahey]

Where are you setting the origin here?

 

[Niner49er52]

say the disk is near the center of the hypotenuse of a right traingle. the spring is attached at the very top of the triangle and is connected to the disk

 

[Niner49er52]

i guess we could say it is at a height h above the ground as well, and if the length of the hypotenuse is L, and the angle is some alpha, then that height would be (L-y)sin(alpha)

 

[Niner49er52]

for the disk itself, it will roll through a distance, or arclength, which is why i first thought the constraint would be its radius times the angle at which it rolls through, theta

 

[Niner49er52]

ive attached a diagram i made of this so it is easier to understand

 

[gabbagabbahey]

Hmmm okay, so the disk is rolling down an incline...is the spring attached to the center of the disk or to a point on the disk's circumference?

$L$ is the distance from the spring's equilibrium point to the bottom of the incline?

is $q$ the distance from the spring equilibrium point to the center of the disk or to a point on the disk's circumference?

 

[Niner49er52]

it is attached to the center of the disk. L is the total distance of the incline. and i made q the direction of motion, it isn't an actual distance in the diagram

 

[Niner49er52]

sorry i realize how that was confusing, i should have made h=(L-q)sin(alpha) rather than that y

 

[Niner49er52]

also forgot to add a value for the unstretched length of the string, i guess l(naught) would work fine