Constraints of a mechanical system

[Ahmed1029]

I'm studying theoretical mechanics and I kind of find the notion of a "mechanical system" very slippery, especially when it comes to constraints. Take an example :

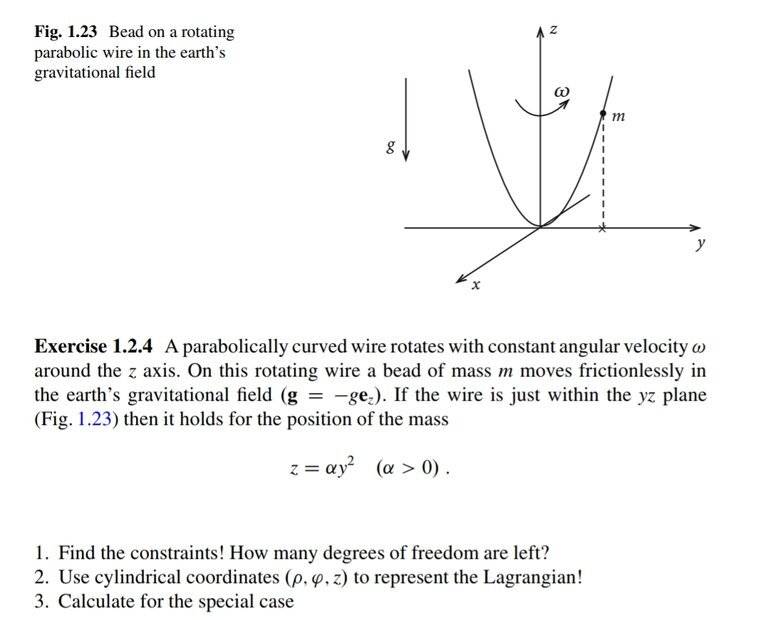
I know that when a system consists of N particles and p constraints, it has 3N-p degrees of freedom; this is the definition. Then I come across something like this example in the picture above, in which I have a wire which includes an infinite number of particles, and in the solution it's completely ignored. Here there are 2 constraints and the auther treated the whole setup as if there is only one particle while the wire is completely ignored, thus the system has one degree if freedom because 3(1)-2=1
In general, how do I know the number of degrees of freedom of a "mechanical system" that is not just made of ordinary accumilatios of discrete particles?

 

[Baluncore]

The wire is a hypothetical perfect guideline for the sliding bead.
Only the position of the bead on the wire is being considered.
The model is applicable to this real situation.
https://en.wikipedia.org/wiki/Liquid-mirror_telescope

 

[Ahmed1029]

The wire is a hypothetical perfect guideline for the sliding bead.
Only the position of the bead on the wire is being considered.
The model is applicable to this real situation.
https://en.wikipedia.org/wiki/Liquid-mirror_telescope

Oh! So it's considered a time dependent geometrical constraint. What about real wires though? Is it right to say that " When I can specify completely the state of a system just by the positions of the discrete particles, then I should ignore any other continuous body as a mere time dependent geometrical constraint"?

 

[vanhees71]

The constraint is a bit inconveniently defined. In cylindrical coordinates it's much simpler and valid for any time,
$$z=\alpha \rho^2.$$
Now first parametrize the position vector (wrt. the inertial frame of reference) of the particle on the parabolic wire and then you can simply put the entire problem into the Lagrangian machinery.

 

[Ahmed1029]

The constraint is a bit inconveniently defined. In cylindrical coordinates it's much simpler and valid for any time,
$$z=\alpha \rho^2.$$
Now first parametrize the position vector (wrt. the inertial frame of reference) of the particle on the parabolic wire and then you can simply put the entire problem into the Lagrangian machinery.

Suppose I don't know which generalized coordinates I should choose to specity the system, but I nevertheless want to know the number of degrees of freedom of the system. In case of discrete particles it's easy, you just find independent equations relating the coordinates to each other until there is no more ( which is done by inspection), then subtract from 3N the number of constraints, where N is the number of particles. Suppose now I have not just discrete particles, but also continuous bodies: How do I know the number of degrees of freedom for sure? My guess is to find any number of coordinates that specify the whole system completely, find the maximum number of equations relating them to each other, and subtract the number of independent equations from the number of original arbitrary coordinates. Is this right.

 

[vanhees71]

That sounds right. A continuous body usually has to be described by fields (e.g., density, velocity, pressure for a fluid). An exception is the rigid body, which has only 6 degrees of freedom (3 position-vector coordinates to any fixed point within the body and 3 Euler angles to describe the rotation of a body-fixed Cartesian coordinate system wrt. a space-fixed Cartesian one). It's a good exercise to derive this with continuum-mechanical methods.