- #1
physics114
- 7
- 0
Correct? Please let me know if my logic is off. =]
Given Problem
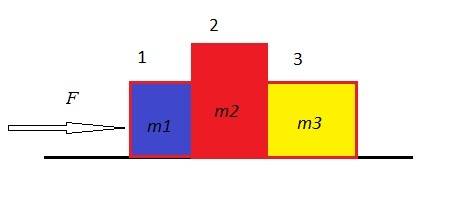
As shown in the figure, a force of magnitude 7.50N pushes three boxes with masses
m1 = 1.30 kg
m2 = 3.20 kg
m3 = 4.30 kg
(a) Find the magnitude of the contact force between boxes 1 and 2. (?N)
(b) Find the magnitude of the contact force between boxes 2 and 3. (?N)
Relevant Equations
F=ma
Strategy?
- Since boxes are in contact, all boxes will have the same acceleration.
- First, find the acceleration given by Newton's 2nd Law. Divide the total horizontal force by the total mass of all three boxes.
- Secondly for (a) and (b) Find individual contact forces by multiplying individual mass with the acceleration found previously.
Attempted Solution
Find contact acceleration
F = ma
a = F/m
a = (7.50N) / (m1+m2+m3)
a = (7.50N) / (1.30kg + 3.20kg + 4.30kg)
a = (7.50N) / (8.8kg)
a = .852273 m/s^2
Part (a)
force between box 1 and box 2
F = ma
F = (3.20kg)*(.852273m/s^2)
F = 2.7272N
Part (b)
force between box 2 and box 3
F = ma
F = (4.30kg)*(.852273m/s^2)
F = 3.66477N
For both parts a and b I was following the example in the book, but don't really understand why we would be multiplying the acceleration with the mass of the box to the right instead of the left. Is this because the force is being applied from left to right and in order to find the contact force (pushing against the overall force) we use the mass of the box exerting the contact force??
Given Problem
As shown in the figure, a force of magnitude 7.50N pushes three boxes with masses
m1 = 1.30 kg
m2 = 3.20 kg
m3 = 4.30 kg
(a) Find the magnitude of the contact force between boxes 1 and 2. (?N)
(b) Find the magnitude of the contact force between boxes 2 and 3. (?N)
Relevant Equations
F=ma
Strategy?
- Since boxes are in contact, all boxes will have the same acceleration.
- First, find the acceleration given by Newton's 2nd Law. Divide the total horizontal force by the total mass of all three boxes.
- Secondly for (a) and (b) Find individual contact forces by multiplying individual mass with the acceleration found previously.
Attempted Solution
Find contact acceleration
F = ma
a = F/m
a = (7.50N) / (m1+m2+m3)
a = (7.50N) / (1.30kg + 3.20kg + 4.30kg)
a = (7.50N) / (8.8kg)
a = .852273 m/s^2
Part (a)
force between box 1 and box 2
F = ma
F = (3.20kg)*(.852273m/s^2)
F = 2.7272N
Part (b)
force between box 2 and box 3
F = ma
F = (4.30kg)*(.852273m/s^2)
F = 3.66477N
For both parts a and b I was following the example in the book, but don't really understand why we would be multiplying the acceleration with the mass of the box to the right instead of the left. Is this because the force is being applied from left to right and in order to find the contact force (pushing against the overall force) we use the mass of the box exerting the contact force??
