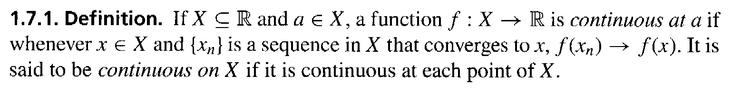Math Amateur
Gold Member
MHB
- 3,920
- 48
I am reading John B. Conway's book: A First Course in Analysis and am focused on Chapter 1: The Real Numbers ... and in particular I am focused on Section 1.7: Continuous Functions ...
I need help with clarifying Definition 1.7.1 ...Definition 1.7.1 reads as follows:
View attachment 9497My question is as follows:
Is the above definition clear and correct? Is it usual?It seems to me Conway has defined continuity at any point $$x \in X$$ ... so why bother mentioning $$a$$ ... ?Can someone please clarify Conway's approach to continuity ...
Peter
I need help with clarifying Definition 1.7.1 ...Definition 1.7.1 reads as follows:
View attachment 9497My question is as follows:
Is the above definition clear and correct? Is it usual?It seems to me Conway has defined continuity at any point $$x \in X$$ ... so why bother mentioning $$a$$ ... ?Can someone please clarify Conway's approach to continuity ...
Peter