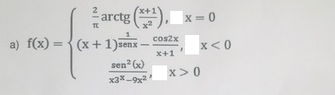- #1
Chipset3600
- 79
- 0
Hello MHB, the f(0) of this function doesn't exist, so I am i wrong or this question don't hv solution?
View attachment 406
View attachment 406