Continuous functions on metric spaces part 2

[Lambda96]

Homework Statement

Show that the mapping $x \mapsto d(x,p)$ is linear.

Relevant Equations

none

Hi,

The task is as follows

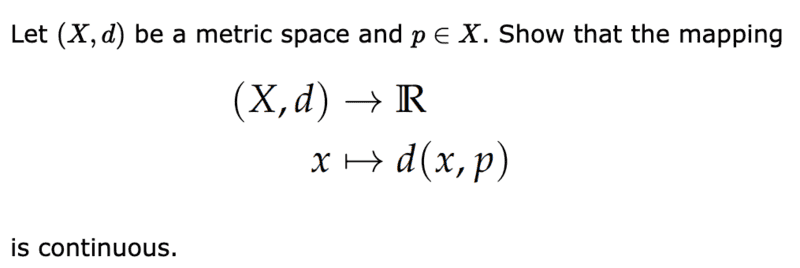
For the proof I wanted to use the boundedness, in the script of my professor the following is given, since both $(X,d)$ and $\mathbb{R}$ are normalized vector spaces

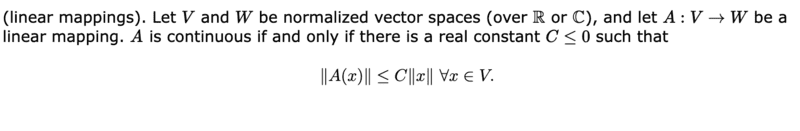
I have now proceeded as follows $|d(x,p)| \le C |x|$ according to Archimedes' principle, a number $C$ now exists, which ensures that the inequality is valid for all $x$.

 

[fresh_42]

$d(\cdot , p)$ isn't linear.

Start with the definition of continuity. Use a function $f$ first, and substitute $f(x)$ with $d(x,p)$ afterwards. So: What does it mean, when a function $f(x)$ is continuous at $x_0$?

 

[pasmith]

$d(\cdot , p)$ isn't linear.

We are not even given that $X$ is a vector space, so we don't have a concept of linearity.

@Lambda96: All you have available to you are the properties of an arbitrary metric and the definition of continuity with respect to that metric. Consider the triangle rule.

 

[Lambda96]

Thank you fresh_42 and pasmith for your help

The continuity of a function $f$ is defined as follows:

A function $f$ is called continuous at the point $x_0$ if for every $\epsilon$ there exists a $\delta$ such that for all $x \in D_f$ with $|x-x_0| < \delta$ : $|f(x) - f(x_0)|< \epsilon$ applies

Do you mean fresh_42 that I should now do the following?

$$|x-x_0| < \delta \rightarrow |d(x,p) - d(x_0,p)|< \epsilon$$

Then I should now determine the $\delta$, right?

 

[fresh_42]

Thank you fresh_42 and pasmith for your help

The continuity of a function $f$ is defined as follows:

A function $f$ is called continuous at the point $x_0$ if for every $\epsilon$ there exists a $\delta$ such that for all $x \in D_f$ with $|x-x_0| < \delta$ : $|f(x) - f(x_0)|< \epsilon$ applies

Do you mean fresh_42 that I should now do the following?

$$|x-x_0| < \delta \rightarrow |d(x,p) - d(x_0,p)|< \epsilon$$

Then I should now determine the $\delta$, right?

Yes, and yes. Use @pasmith's hint. The triangle inequality is basically all we have. Note that $|x-x_0|=d(x,x_0).$

 

[Lambda96]

Thank you fresh_42 for your help


The triangle inequality is as follows $d(x,x_0) \le d(x,p) + d(p,x_0)$


With the triangle inequality you can then set up the two inequalities $d(x,p) - d(p,x_0) \le d(x,x_0)$ and $d(p,x_0)- d(x,p) \le d(x,x_0)$ from this then follows $|d(x,p) - (p,x_0)| \le d(x,x_0)$

The following $|d(x,p)- d(p,x_0)| < \epsilon$ holds and because of $|d(x,p) - (p,x_0)| \le d(x,x_0)$ with $|x-x_0|=d(x,x_0)$ then $\delta=\epsilon$ follows

 

[PeroK]

Thank you fresh_42 for your help


The triangle inequality is as follows $d(x,x_0) \le d(x,p) + d(p,x_0)$


With the triangle inequality you can then set up the two inequalities $d(x,p) - d(p,x_0) \le d(x,x_0)$ and $d(p,x_0)- d(x,p) \le d(x,x_0)$ from this then follows $|d(x,p) - (p,x_0)| \le d(x,x_0)$

The following $|d(x,p)- d(p,x_0)| < \epsilon$ holds and because of $|d(x,p) - (p,x_0)| \le d(x,x_0)$ with $|x-x_0|=d(x,x_0)$ then $\delta=\epsilon$ follows

I'll make this general comment for the last time. You are not thinking through these problems in terms of what you are trying to prove. Your work is superficial, IMO. It's not that you need detail, as such, but that you need to be much clearer about the steps required in the proof.

In this case, specifically, you didn't say that for a function to be continuous, we mean that it is continuous at every point $x_0 \in X$. You might say you knew that. But, I'm not convinced that you recognised that.

So, your proof should start: "Let $x_0 \in X$ and $\epsilon > 0$.

PS Having a coherent, logical structure to your proof is a good habit to get into.

 

[Lambda96]

Thanks PeroK for the tip

Unfortunately, I forgot to say in my calculation that I was only interested with the calculation of how to determine the $\delta$. In my documents I have provided complete proof

 

[pasmith]

In fact we have uniform continuity, since $\delta = \epsilon$ works independently of $x$.