Fermat1
- 180
- 0
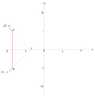
Calculate the integral of $1/z$ around $C$, where $C$ is any contour going from $-\sqrt{3}+i$ to $-\sqrt{3}-i$ and is contained in the set of complex numbers whose real part is negative.
My answer: Let $f=1/z$ Then $f$ has a simple pole at $z=0$ with residue 1. How do I calculate the winding number so I can use the residue formula?
Thanks
My answer: Let $f=1/z$ Then $f$ has a simple pole at $z=0$ with residue 1. How do I calculate the winding number so I can use the residue formula?
Thanks