Contour integration in propagator

[ianhoolihan]

Hi all,

I've been playing around with (2.54) of Peskin and Schroeder, and I've some quick questions about it. Firstly, the part I'm stuck on:

$$\int\frac{d^3p}{(2\pi)^3}\left[\left.\frac{1}{2E_p}e^{-ip\cdot (x - y)}\right|_{p^0=E_p} - \left.\frac{1}{-2E_p}e^{-ip\cdot (x - y)}\right|_{p^0=-E_p}\right]={x^0>y^0} \int\frac{d^3p}{(2\pi)^3}\int\frac{dp^0}{2\pi i}\ \frac{-1}{p^2 - m^2}e^{-ip\cdot (x - y)}$$

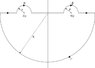
where the contour for the last integral is shown here http://en.wikipedia.org/wiki/Propagator#Causal_propagator.

My first question is to check that the factor of $-1$ in the second term is since the contour is clockwise if we close below, unlike the usual anticlockwise? I'm using the residue theorem here, not the Cauchy integral formula.

Secondly, how does $x^0>y^0$ come in? PS assume it when they say that
$$\langle|0|[\phi(x),\phi(y)]|0\rangle = \int\frac{d^3p}{(2\pi)^3}\frac{1}{2E_p}\left(e^{-ip\cdot (x - y)} + e^{ip\cdot (x - y)}\right)$$
but I'm not sure if the assumption $x^0>y^0$ is required in this equation, or in the future integration steps.

The answer to the above might affect the next question, but PS say that, to evaluate the case for $y^0>x^0$, one closes the integral above, which gives zero. Why don't they just flip the integral upside down, so it's non-zero? I assume there is a physical reason such as causality that makes us want to be zero, but could someone explain this?

Cheers

 

[ianhoolihan]

I thought I'd solved the following problem, but I guess not:

I understand that, using the residue theorem, one can get the integral around the curve that closes from below. However, I am not sure how to convert that into a $dp^0$ integral, as the poles lie on this line, and if I recall correctly, theorems for contour integration require the poles to lie in the interior of a region.

I would understand displacing the poles by $\pm i\epsilon$ and then letting $\epsilon \to 0$, which seems to be what Wikipedia indicates. Is this what Peskin and Schroeder do, just without explicitly mentioning it?

My prior questions still stand as well.

Cheers

 

[strangerep]

My first question is to check that the factor of $-1$ in the second term is since the contour is clockwise if we close below, unlike the usual anticlockwise?

That sounds right (though I'd have to recheck the full calculation to make sure -- it's quite a few years now since I did it myself).

Secondly, how does $x^0>y^0$ come in? [...]

The answer to the above might affect the next question, but PS say that, to evaluate the case for $y^0>x^0$, one closes the integral above, which gives zero. Why don't they just flip the integral upside down, so it's non-zero?

To evaluate the contour integral, the contribution from the large semicircle at infinity must vanish. For a given sign of the exponent, this happens in one halfplane, but not the other.

 

[strangerep]

I understand that, using the residue theorem, one can get the integral around the curve that closes from below. However, I am not sure how to convert that into a $dp^0$ integral, as the poles lie on this line, and if I recall correctly, theorems for contour integration require the poles to lie in the interior of a region.

Yes, the residues of only the poles interior to the contour contribute.

I would understand displacing the poles by $\pm i\epsilon$ and then letting $\epsilon \to 0$, which seems to be what Wikipedia indicates. Is this what Peskin and Schroeder do, just without explicitly mentioning it?

That also sounds right. Sometimes people tilt the real axis by an infinitesimal amount to shorten the calculation. Others cheat (imho) by displacing the poles by an infinitesimal imaginary amount. Personally, I don't like either of these shortcuts and its more reliable to use small semicircles around the pole(s), as you said, and then evaluate the contribution on the small semicircle in the limit of zero radius. The result of the integral should then be the same regardless of which way you deform the contour, provided the contributions on the small semicircles are both evaluated correctly.

If you can cough up a few bucks, by your own copy of this inexpensive textbook. :-)
https://www.amazon.com/dp/0071615695/?tag=pfamazon01-20
It's quite useful for checking whether integrands do/don't vanish on the large and small semicircles in these sorts of contour integrals.

 

[ianhoolihan]

To evaluate the contour integral, the contribution from the large semicircle at infinity must vanish. For a given sign of the exponent, this happens in one halfplane, but not the other.

Ah, so simple! I didn't bother checking the limits for the arc as I was confused with the following point...

Yes, the residues of only the poles interior to the contour contribute.
That also sounds right. Sometimes people tilt the real axis by an infinitesimal amount to shorten the calculation. Others cheat (imho) by displacing the poles by an infinitesimal imaginary amount. Personally, I don't like either of these shortcuts and its more reliable to use small semicircles around the pole(s), as you said, and then evaluate the contribution on the small semicircle in the limit of zero radius. The result of the integral should then be the same regardless of which way you deform the contour, provided the contributions on the small semicircles are both evaluated correctly.

Hmmm, I agree. That feels like cheating. I am not sure how using the semicircles around the poles differs from the case of displacing the poles slightly. In the case of slightly displaced poles, at least there are no poles on the real axis. With the semicircles, there are poles on the flat edge, so one cannot evaluate the integrals...so don't the poles need to be displaced anyway?

Anyway, thanks a heap for that clarification strangerep,

Ianhoolihan.

PS --- that books looks really good, as it seems to be based around solved examples.

 

[vanhees71]

To precisely decide which propagator (there are many different propagators; in vacuum QFT you usually want the time-ordered propagator, which in this case is identical with the Feynman propagator; in linear-response theory you need the retareded propagator, etc.) you want to calculate, you should either give a clear contour in complex $p^0$ plane or an appropriate regularization by displacing the poles. Usually the latter form is more convenient for calculations.

For more details on different propagators in the real-time Schwinger-Keldysh formalism of relativistic many-body theory, you can find here:

http://fias.uni-frankfurt.de/~hees/publ/green.pdf

 

[strangerep]

I am not sure how using the semicircles around the poles differs from the case of displacing the poles slightly.

In the case where the contribution from the small semicircle vanishes in the limit of zero radius, they'll be the same. (Sorry I don't have more spare time -- it would be helpful to do all these integrals explicitly once and for all -- and post them somewhere -- since I've seen such questions re-asked here several times.)

PS --- that [Schaum Outline book] looks really good, as it seems to be based around solved examples.

Actually, I might have been thinking of this one:
https://www.amazon.com/dp/B000720BX2/?tag=pfamazon01-20

which is out of print now -- but Amazon shows some used copies at reasonable price. The new edition's price is a bit excessive, though.

Anyway, between the two of them, it should be easy to review basic contour integral stuff.

 

[ianhoolihan]

To precisely decide which propagator (there are many different propagators; in vacuum QFT you usually want the time-ordered propagator, which in this case is identical with the Feynman propagator; in linear-response theory you need the retareded propagator, etc.) you want to calculate, you should either give a clear contour in complex $p^0$ plane or an appropriate regularization by displacing the poles. Usually the latter form is more convenient for calculations.

For more details on different propagators in the real-time Schwinger-Keldysh formalism of relativistic many-body theory, you can find here:

http://fias.uni-frankfurt.de/~hees/publ/green.pdf

It doesn't sit that well with me that the propagator depends on the choice of contour, but I guess I'll have to read further before I have an informed opinion.

 

[ianhoolihan]

In the case where the contribution from the small semicircle vanishes in the limit of zero radius, they'll be the same. (Sorry I don't have more spare time -- it would be helpful to do all these integrals explicitly once and for all -- and post them somewhere -- since I've seen such questions re-asked here several times.)

OK, since I'm doing it explicitly myself, I'll post as much as I can here, and hopefully all you have to do is say "Correct!"

Using the figure below, we'll close the contour below with an arc C of radius R, and let the two semicircles be $\alpha$ and $\beta$ about the poles at $E_p$ and $-E_p$, of radius $\epsilon$ and $\rho$, respectively, so that the total contour is
$$\oint_{Total} = \int_{-R}^{-E_p-\epsilon}dp^0 + \int_\alpha + \int_{-E_p+\epsilon}^{E_p-\rho}dp^0 + \int_\beta + \int_{E_p+\rho}^R + \int_C$$.
Now, let's evaluate the separate parts for the function
$$\frac{-1}{z^2 -E_p^2} e^{-iz(x^0-y^0) -i\mathbf{p}\cdot(\mathbf{x-y})}$$
where we use coordinates $z=p^0 + iv$.

Firstly, we are going to use the residue theorem, so note that
$$\frac{-1}{z^2 -E_p^2} e^{-iz(x^0-y^0) -i\mathbf{p}\cdot(\mathbf{x-y})} = \frac{-1}{(z-E_p)(z+E_p)} e^{-iz(x^0-y^0) -i\mathbf{p}\cdot(\mathbf{x-y})}$$
so has poles at $\pm E_p$ with residues $(-1/2E_p)\ e^{-iE_p(x^0-y^0) -i\mathbf{p}\cdot(\mathbf{x-y})}$ and $(+1/2E_p)\ e^{+iE_p(x^0-y^0) -i\mathbf{p}\cdot(\mathbf{x-y})}$. Hence, the residue theorem tells us that
$$\oint_{Total} \frac{-1}{z^2 -E_p^2} e^{-iz(x^0-y^0) -i\mathbf{p}\cdot(\mathbf{x-y})} = -\frac{2\pi i}{2E_p}\left[-e^{-iE_p(x^0-y^0) -i\mathbf{p}\cdot(\mathbf{x-y})} + \ e^{+iE_p(x^0-y^0) -i\mathbf{p}\cdot(\mathbf{x-y})}\right].
$$
(Note the minus sign as we're going the wrong way round the contour.)

Secondly, for the large arc C, we can use Jordan's lemma. Note that, for sufficiently large R,
$$\left|\frac{-1}{z^2 - E_p^2} e^{-ip\cdot(x-y)}\right|= \frac{1}{R^2-E_p^2}\quad\forall |z|=R$$
which clearly tends to zero as $R\to \infty$. Furthermore, given that we have a lower semicircular integral of the form
$$\int_C e^{-iaz}f(z)dz$$
then as long as $a>0$, we may apply Jordan's lemma. That is,
$$\int_C \frac{-1}{z^2 - E_p^2} e^{-iz(x^0-y^0) -i\mathbf{p}\cdot(\mathbf{x-y})} \to 0\quad\text{as }R\to\infty$$
as long as $x^0-y^0>0$. So that first piece is solved.

Finally, let's consider the contour around $\alpha$, which we parameterise by $z = -E_p + \epsilon e^{i\theta}$. Hence
$$\int_\alpha \frac{-1}{z^2 -E_p^2} e^{-iz(x^0-y^0) -i\mathbf{p}\cdot(\mathbf{x-y})} = -\int_0^\pi d\theta i\epsilon e^{i\theta} \frac{-1}{(-E_p + \epsilon e^{i\theta})^2 -E_p^2} e^{-i(-E_p + \epsilon e^{i\theta})(x^0-y^0) -i\mathbf{p}\cdot(\mathbf{x-y})}= i\int_0^\pi d\theta \frac{1}{(\epsilon e^{i\theta}-2E_p)} e^{iE_p(x^0-y^0) + i\epsilon e^{i\theta}(x^0-y^0) -i\mathbf{p}\cdot(\mathbf{x-y})}$$
(Note the extra minus as we're going the wrong way round the contour.) Now, as $\epsilon\to 0$ we see
$$\lim_{\epsilon\to 0}\int_\alpha \frac{-1}{z^2 -E_p^2} e^{-iz(x^0-y^0) -i\mathbf{p}\cdot(\mathbf{x-y})} = i\pi\frac{1}{-2E_p} e^{+iE_p(x^0-y^0) -i\mathbf{p}\cdot(\mathbf{x-y})}=i\pi Res(-E_p)$$
(Note that this result is a general one.) Similarly for $\beta$
$$\lim_{\rho\to 0}\int_\beta \frac{-1}{z^2 -E_p^2} e^{-iz(x^0-y^0) -i\mathbf{p}\cdot(\mathbf{x-y})} = i\pi\frac{1}{2E_p} e^{-iE_p(x^0-y^0) -i\mathbf{p}\cdot(\mathbf{x-y})}=i\pi Res(E_p)$$

The last thing we need is the concept of the Cauchy principal value integral: http://mathworld.wolfram.com/CauchyPrincipalValue.html, which means that
$$P.V.\int_{-R}^R dp^0 = \lim_{\epsilon\to 0,\rho\to 0}\left[\int_{-R}^{-E_p-\epsilon}dp^0 + \int_{-E_p+\epsilon}^{E_p-\rho}dp^0+\int_{E_p+\rho}^R dp^0\right].$$

Finally, putting everything together in the limits $\epsilon\to 0,\ \rho\to 0,\ R\to \infty$ gives
$$P.V.\int_{-\infty}^\infty dp^0 = \oint_{Total}-\int_\alpha-\int_\beta -\int_C = -\frac{2\pi i}{2E_p}\left[-e^{-iE_p(x^0-y^0) -i\mathbf{p}\cdot(\mathbf{x-y})} + \ e^{+iE_p(x^0-y^0) -i\mathbf{p}\cdot(\mathbf{x-y})}\right] - i\pi\frac{1}{-2E_p} e^{+iE_p(x^0-y^0) -i\mathbf{p}\cdot(\mathbf{x-y})} -i\pi\frac{1}{2E_p} e^{-iE_p(x^0-y^0) -i\mathbf{p}\cdot(\mathbf{x-y})} - 0$$

That is
$$P.V.\int dp^0\ \frac{-1}{p^2 -m^2} e^{-ip\cdot(x-y)} = \frac{\pi i}{2E_p}\left[e^{-iE_p(x^0-y^0) -i\mathbf{p}\cdot(\mathbf{x-y})} - \ e^{+iE_p(x^0-y^0) -i\mathbf{p}\cdot(\mathbf{x-y})}\right].$$

Unfortunately I am out by a factor of two from the correct answer of (2.54) in PS. However, I am way past tired, so need to hit the hay --- if somebody finds my error, I'd appreciate if you can let me know, and I'll edit my post tomorrow.

Furthermore, note how I've only got the result for the principal value integral...I recall reading somewhere that it equals the usual integral if it the function is Lebesgue-integrable. I don't know what this means, but if someone does, and could confirm the function in question is, I'd be tickled pink.

Lastly, I haven't read this yet, but the following describes how the "cheating" strangerep was referring to may actually be notational (see page 14 or so of pdf): http://hitoshi.berkeley.edu/221a/contour.pdf.

 

[strangerep]

At this stage, I'll just make a few suggestions...

1) You can factor out the exponential involving spatial components.
So they don't affect the energy integral.

2) You can cut down on the mess enormously by using some different symbols
for the purposes of performing the integral. E.g., you could start with
$$ \int\!dz\; \frac{e^{ikz}}{z^2 - a^2} $$ where $k,a$ are both real.
That should reduce your typing considerably.

3) Your application of Jordan's lemma is a bit sloppy, since you don't
actually evaluate the the maximum value of the denominator on the large
semicircle.

4) Your treatment of the small semicircles around the poles is quite wrong.
You can't use the residue theorem here unless you've got a closed circle
around the poles, but you've only got two little semicircles. (The treatment
in that contour.pdf file you linked to is sloppy in this regard, since it
assumes certain symmetry on the upper and lower sides of each pole.)
To do it properly, you'll need to do each semicircle properly as a line integral.
Set $z=r e^{i\theta}$ with $r$ constant, and do a $\theta$ integration
accordingly. The integrand must be Laurent-expanded around each pole first,
so that you can subsequently take a limit as $r\to 0$.

5) If you use a slightly different contour by avoiding the poles via
semicircles in the lower half plane, you won't have to evaluate any residues
at all, since the new contour encloses no poles. If you evaluate the small
line integrals correctly, you'll get the right answer.

6) I just found my old notes where I evaluated this same integral, so I can
probably post it if you get stuck. Item 5 above can be a bit tricky if you
haven't seen it done before, but I'll let you have a go at it first. :-)

7) Regarding the Lebesgue-integrable thing... it's insensitive to integration
on "sets of measure zero" (i.e., single points in this case). So you can
exclude the isolated poles on the real axis. I hope that makes sense.

 

[ianhoolihan]

At this stage, I'll just make a few suggestions...

1) You can factor out the exponential involving spatial components.
So they don't affect the energy integral.

2) You can cut down on the mess enormously by using some different symbols
for the purposes of performing the integral. E.g., you could start with
$$ \int\!dz\; \frac{e^{ikz}}{z^2 - a^2} $$ where $k,a$ are both real.
That should reduce your typing considerably.

True. That would make things a lot neater. My mistake.

3) Your application of Jordan's lemma is a bit sloppy, since you don't
actually evaluate the the maximum value of the denominator on the large
semicircle.

OK, my notes say that as long as there is an upper bound such that the integral is less than or equal to it for all $|z|=R$ then one can use Jordan's lemma. When you say I haven't evaluated it, is it not $1/(R^2 - E_p^2)$? (I was assuming $E_p = \sqrt{\mathbf{p}^2 +m^2}$ was constant...)

4) Your treatment of the small semicircles around the poles is quite wrong.
You can't use the residue theorem here unless you've got a closed circle
around the poles, but you've only got two little semicircles. (The treatment
in that contour.pdf file you linked to is sloppy in this regard, since it
assumes certain symmetry on the upper and lower sides of each pole.)
To do it properly, you'll need to do each semicircle properly as a line integral.
Set $z=r e^{i\theta}$ with $r$ constant, and do a $\theta$ integration
accordingly. The integrand must be Laurent-expanded around each pole first,
so that you can subsequently take a limit as $r\to 0$.

I only used the residue theorem for the complete closed loop integral, which certainly includes the two poles. So I don't follow that point.

Secondly, I did parameterise each semicircle exactly as you said. I'm not sure if what I did was "Laurent-expanded", but it seems right to me. So I don't really follow this point either.

5) If you use a slightly different contour by avoiding the poles via
semicircles in the lower half plane, you won't have to evaluate any residues
at all, since the new contour encloses no poles. If you evaluate the small
line integrals correctly, you'll get the right answer.

OK, true, that would be quicker. Thinking in my head, the integrals on the semicircles would change sign from what I gave in the last post, and that gives ... the same answer I originally had. I believe this is wrong, as it is a factor of two out from the top equation of (2.54) on page 30 of PS. Maybe it isn't...

6) I just found my old notes where I evaluated this same integral, so I can
probably post it if you get stuck. Item 5 above can be a bit tricky if you
haven't seen it done before, but I'll let you have a go at it first. :-)

I think I've addressed your points, and I'm not sure if I'm as wrong as I felt initially... I think I did the integration on the semicircles correctly, but maybe you skimmed over it?

7) Regarding the Lebesgue-integrable thing... it's insensitive to integration
on "sets of measure zero" (i.e., single points in this case). So you can
exclude the isolated poles on the real axis. I hope that makes sense.

Not really...does this mean that the principal value is equal to the normal integral?

 

[vanhees71]

I haven't followed your long calculation in detail. What's for sure is that you calculate the retarded propagator if you use the contour depicted in #9. In the following I name this contour $\mathcal{C}_{\text{ret}}$. To see that you get the retarded propagator, you do the integral along the contour by closing it with large semicircles in the upper (lower) $p_0$-half-plane such that due to the exponential of the Fourier integral, which is the Mills representation of the free vacuum propagator of a scalar field,
$$\tilde{G}_{\text{ret}}(t,\vec{p})=\int_{\mathcal{C}_{\text{ret}}} \frac{\mathrm{d} p_0}{2 \pi} \frac{\exp(-\mathrm{i} p_0 t)}{p_0^2-\omega^2}$$
the contribution of these additional circles becomes 0 in the limit of infinite radius, i.e., you have to close the contour for $t<0$ in the upper and for $t>0$ in the lower half-plain. Since there are no poles inside the loop for $t<0$ you have
$$\tilde{G}_{\text{ret}}(t,\vec{p}) \propto \Theta(t).$$
For $t>0$ you pick up both poles of the integrand. Due to the residue theorem you have
$$G_{\text{ret}}(t,\vec{p})=-\Theta(t) \mathrm{i} \left [\frac{\exp(-\mathrm{i} \omega t)}{2 \omega} - \frac{\exp(\mathrm{i}\omega t)}{2 \omega} \right ] =-\Theta(t) \frac{\sin(\omega t)}{\omega}.$$
Of course, in the whole calculation $\omega=\sqrt{\vec{p}^2+m^2}.$ The sign comes from the clockwise, i.e., negative orientation of the contour in the complex plane.

It is easy to check that the Mills representation obeys the equation for the Green's function of the KG equation, i.e.,
$$(\partial_t^2+\omega^2) \tilde{G}_{\text{ret}} ( t, \vec{p} )=-\delta(t),$$
corresponding to the equation in position representation
$$(\Box+m^2) G(t,\vec{x})=-\delta^{(4)}(x).$$
In energy-momentum representation you can alternatively write
$$\bar{G}_{\text{ret}}(p)=\frac{1}{(p_0+\mathrm{i} 0^+)^2-\omega^2} = \frac{1}{p^2-m^2+\mathrm{i} \mathrm{sign}(p_0) 0^+.}$$
This shifts the poles in the complex $p_0$ plane both infintesimally into the lower plane. Now you can integrate along the real axis and do the same calculation again, closing the contour as shown above. You'll get the same result as before.

What you usually need in the Feynman rules of vacuum quantum field theory is a slightly different propagator. This propagator is uniquely defined by the time ordering prescription, which comes from the Dyson series of the time-evolution operator in the interaction picture due to Wick's theorem. The corresponding propagator is the socalled causal propagator. In the vacuum it's at the same time the Feynman propagator that is defined that the particles correspond to positive energies and are propagated according to the retarded propagator and the antiparticles (or holes) are propagated according to the advanced propgator. In time-position representation the definition is
$$G_{c}(t,\vec{x})=-\mathrm{i} \langle \Omega|\mathcal{T} \hat{\phi}(t,\vec{x}) \hat{\phi}^{\dagger}(0)| \Omega \rangle.$$
Using the mode decomposition of the quantum fields into creation and annihilation operators wrt. the one-particle momentum eigenstate basis, you find
$$\bar{G}_c(p)=\frac{1}{p^2-m^2 + \mathrm{i} 0^+}.$$
By closing the contour for the $p_0$ integration you get for the Mills representation
$$\tilde{G}(t,\vec{p})=-\mathrm{i} \Theta(t) \frac{\exp(-\mathrm{i} \omega t)}{2 \omega} - \mathrm{i} \Theta(-t) \frac{\exp(+\mathrm{i} \omega t)}{2 \omega}=-\mathrm{i}\frac{\exp(-\mathrm{i} \omega |t|)}{2 \omega}.$$

 

[ianhoolihan]

Thanks vanhees, the effort is much appreciated. However, at the moment I'm still stuck on the position integral, not momentum. Your post will be most helpful when I spend more time of the link between the two. (I was stuck on (2.57) and the following equation in PS for a while, especially why there is the opposite sign to normal in the Fourier transform.)

Two points though:

Firstly, I had problems with the following:

$$\bar{G}_{\text{ret}}(p)=\frac{1}{(p_0+\mathrm{i} 0^+)^2-\omega^2} = \frac{1}{p^2-m^2+\mathrm{i} \mathrm{sign}(p_0) 0^+.}$$

When you expand the LHS demominator out, there is a term $2ip^0 0^+$. Is the reason you only put $i\mathrm{sign}(p^0)0^+$ because the size of $p^0$ is irrelevant, given the limit $0^+$? The reason I bring it up is because every other time I've seen the equation, the $\mathrm{sign}(p^0)$ part is left out...

Lastly, something trivial: did you miss a subscript "c" on the propagator in your last equation?

 

[strangerep]

[...] I think I did the integration on the semicircles correctly, but maybe you skimmed over it?

Unbelievable! Now it's my turn to use the "I was way past tired" excuse. Yes, I did indeed skim too fast. (Maybe I wouldn't have if there weren't so many symbols floating around, but, oh, that's a lame excuse.) I'll try to check your factors of 2 later after I wipe the egg off my face.

 

[vanhees71]

Thanks vanhees, the effort is much appreciated. However, at the moment I'm still stuck on the position integral, not momentum.

The full transform from energy-momentum to time-position representation is not that easy. You have to calculate (take the time-ordered propagator as an example)
$$G_c(t,\vec{x})=\int_{\mathbb{R}^4} \frac{\mathrm{d}^4 p}{(2 \pi)^4} \frac{\exp(-\mathrm{i} p \cdot x)}{p^2-m^2+\mathrm{i} 0^+}.$$
This is pretty involved and leads to modified Bessel functions (except in the massless case, where you get $\delta$ distributions).

To simplify the task you can use the fact that the Green's functions are Lorentz scalars (under proper orthochronous Lorentz transformations). Thus you can evaluate the integral for special choices of $x$ and then write it covariantly to get the general case. Unfortunately, there are singularities along the light cone, and you have to investigate spacelike ($x^2<0$) and timelike ($x^2>0$) space-time arguments separately. In the latter case you can set $\vec{x}=0$ in the former $t=0, \quad \vec{x}=(0,0,r)$.

You find these calculations in older textbooks, where the space-time formulation is treated in more detail then in modern ones, e.g., in Bjorken Drell, Schweber, or Bogoliubov Shirkov.

Two points though:

Firstly, I had problems with the following:

$$\bar{G}_{\text{ret}}(p)=\frac{1}{(p_0+\mathrm{i} 0^+)^2-\omega^2} = \frac{1}{p^2-m^2+\mathrm{i} \mathrm{sign}(p_0) 0^+.}$$

When you expand the LHS demominator out, there is a term $2ip^0 0^+$. Is the reason you only put $i\mathrm{sign}(p^0)0^+$ because the size of $p^0$ is irrelevant, given the limit $0^+$? The reason I bring it up is because every other time I've seen the equation, the $\mathrm{sign}(p^0)$ part is left out...

That's correct. Of course you can as well write $\mathrm{i} p_0 0^+$.

Lastly, something trivial: did you miss a subscript "c" on the propagator in your last equation?

Yes, I did. I added these subscript "ret" and "c" to clearly indicate the different propagators.

 

[strangerep]

[...]Unfortunately I am out by a factor of two from
the correct answer of (2.54) in PS.

I now think the expression (2.54) in PS is wrong, and should in fact have
the following denominator in the integrand:
$$
p^2 - m^2 + i\epsilon p^0
$$
This corresponds to Scharf, eq(2.3.22). The extra $\epsilon$ terms shifts
both poles into the lower halfplane, so you don't need the little semicircles
to avoid them on the real axis.

However, this also means that there's some other fudges floating around, since
the 3D integral should then involve
$$
\frac{1}{E_p - i\epsilon}
$$
and
$$
\frac{1}{-E_p - i\epsilon}
$$
and blithely ignoring the $\epsilon$ terms at this point is unjustified.

BTW, note that the above from the Feynman prescription where we use the
denominator
$$
p^2 - m^2 + i\epsilon
$$
which moves one pole up and the other down.

OTOH, the factor of 2 can probably be corrected in a better way by starting
the whole relativistic field formalism using an appropriately normalized measure
on the +ve energy mass shell. But that's a story for another day.

 

[ianhoolihan]

The full transform from energy-momentum to time-position representation is not that easy...

I was actually starting from the time-position basis as in Peskin and Schroeder. I'd then transform to energy-momentum. Nonetheless, you've given me a lot to think about!

Unbelievable! Now it's my turn to use the "I was way past tired" excuse. Yes, I did indeed skim too fast. (Maybe I wouldn't have if there weren't so many symbols floating around, but, oh, that's a lame excuse.) I'll try to check your factors of 2 later after I wipe the egg off my face.

That makes my late night feel a little less of a waste!

I now think the expression (2.54) in PS is wrong, and should in fact have
the following denominator in the integrand:
$$
p^2 - m^2 + i\epsilon p^0
$$
This corresponds to Scharf, eq(2.3.22). The extra $\epsilon$ terms shifts
both poles into the lower halfplane, so you don't need the little semicircles
to avoid them on the real axis.

However, this also means that there's some other fudges floating around, since
the 3D integral should then involve
$$
\frac{1}{E_p - i\epsilon}
$$
and
$$
\frac{1}{-E_p - i\epsilon}
$$
and blithely ignoring the $\epsilon$ terms at this point is unjustified.

BTW, note that the above from the Feynman prescription where we use the
denominator
$$
p^2 - m^2 + i\epsilon
$$
which moves one pole up and the other down.

OTOH, the factor of 2 can probably be corrected in a better way by starting
the whole relativistic field formalism using an appropriately normalized measure
on the +ve energy mass shell. But that's a story for another day.

OK, you've given me a lot to read up on, which I'll get to soon. I'm especially interested that you think PS is wrong. Also, this "appropriately normalized measure on the +ve energy mass shell..." is new to me, as I thought things were already nicely normalised? (Is what you are referring to a mainstream idea?)

Oh, would you say my process of evaluating the integral was correct, and the factor of two was not an error in my calculations?

Cheers strangerep.

 

[strangerep]

I'm especially interested that you think PS is wrong.
[...] would you say my process of evaluating the integral was correct,
and the factor of two was not an error in my calculations?

My recent boo-boo makes me too shy to utter any strong statements for a while.
But if you've still got energy, you could check my results by doing
the following exercise:

Start with the simpler integral I mentioned earlier, i.e.,
$$I_1 ~:=~ \int_{-\infty}^{+\infty} \!\! dz \; \frac{e^{ikz}}{z^2 - a^2}$$
where $k,a$ are real nonzero constants, with $k>0$.
(But don't refer to your previous work while doing this, so as not to bias the calculation.)
Do it two ways:

1) with a contour that takes little detours around the poles in the upper halfplane (and hence encloses both poles),

2) with a contour that takes little detours around the poles in the lower halfplane (and hence encloses no poles).

Do you get the same answer in both cases, and is the answer compatible with what you had before?

Then do it twice more with modified denominators:

(i) $z^2 - a^2 + i\epsilon z$

(ii) $z^2 - a^2 + i\epsilon$

Check where each of these moves the poles, and what the contour integral results are in both cases.

Also, this "appropriately normalized measure on the +ve energy mass shell..." is new to me, as I thought things were already nicely normalised? (Is what you are referring to a mainstream idea?)

It arises if one constructs QFT by causal +ve energy Poincare representations. One needs an integration measure over the +ve energy mass shell of the form
$$
\int\! d^4p \; \delta(p^2-m^2) \; \Theta(p_0)
$$
except that some constant factors are needed in order to end up with the usual 3D integral formulas and covariant commutation relations. Scharf also talks about integrals of this form -- which are closely related to all the stuff we've been talking about here.

 

[ianhoolihan]

Start with the simpler integral I mentioned earlier, i.e.,
$$I_1 ~:=~ \int_{-\infty}^{+\infty} \!\! dz \; \frac{e^{ikz}}{z^2 - a^2}$$
where $k,a$ are real nonzero constants, with $k>0$.
(But don't refer to your previous work while doing this, so as not to bias the calculation.)
Do it two ways:

1) with a contour that takes little detours around the poles in the upper halfplane (and hence encloses both poles),

2) with a contour that takes little detours around the poles in the lower halfplane (and hence encloses no poles).

Do you get the same answer in both cases, and is the answer compatible with what you had before?

I get
$$I_1 = -\frac{i\pi}{2a}\left(e^{ika}-e^{-ika}\right) = \frac{\pi}{a}\sin{ka}$$
in both cases, which is compatible with what I previously had.

Then do it twice more with modified denominators:

(i) $z^2 - a^2 + i\epsilon z$

OK, I will be pedantic for now, such that, the poles are at
$$z= \frac{-i\epsilon}{2}\pm \sqrt{a^2-\frac{\epsilon^2}{4}},$$
i.e. they're shifted into lower half plane (and displaced slightly on real axis as well).

The residue theorem (with the assumption that the arc of semicircle goes to zero, which I haven't checked) then gives
$$\int_{-\infty}^{+\infty} \!\! dz \; \frac{e^{ikz}}{z^2 - a^2+i\epsilon z} = -\frac{2\pi i}{\alpha_1 - \alpha_2}\left(e^{ik\alpha_1} - e^{ik\alpha_2}\right)\quad\text{where}\quad \alpha_1 = -\frac{i\epsilon}{2}+\sqrt{a^2-\frac{\epsilon^2}{4}},\ \ \alpha_2 = -\frac{i\epsilon}{2}-\sqrt{a^2-\frac{\epsilon^2}{4}}.$$
Now, in the limit $\epsilon \to 0$, $\alpha_1 \to a$ and $\alpha_2 \to -a$, and hence
$$\lim_{\epsilon \to 0}\int_{-\infty}^{+\infty} \!\! dz \; \frac{e^{ikz}}{z^2 - a^2+i\epsilon z} = -\frac{\pi i}{a}\left(e^{ika} - e^{-ika}\right)$$
which (hey presto!) is as before, but with the factor of two problem fixed, so it will agree with PS. So, it looks like we agree PS may be wrong...

(ii) $z^2 - a^2 + i\epsilon$

OK, now the the poles are at
$$z=\pm re^{i\theta}\quad\text{where}\quad r=(a^4 + \epsilon^2)^{\frac{1}{4}},\ \ \theta=-\frac{1}{2}\tan^{-1}\left(\frac{\epsilon}{a^2}\right).$$
That is, the one with positive real component is in the lower half plane, and the one with negative real component is in the upper half plane. That means there will be only one residue inside the contour (semicircle in lower half plane), so
$$\int_{-\infty}^{+\infty} \!\! dz \; \frac{e^{ikz}}{z^2 - a^2+i\epsilon} = -2\pi i \frac{e^{ik re^{i\theta}}}{2 r e^{i\theta}}.$$
As $\epsilon \to 0,\ r\to a,\ \theta \to 0$ so
$$\lim_{\epsilon \to 0}\int_{-\infty}^{+\infty} \!\! dz \; \frac{e^{ikz}}{z^2 - a^2+i\epsilon} = -\frac{\pi i}{a} e^{ika}$$
which, unless I've made an error, is the same apart from the missing negative exponential term.

So, to vanhees71 --- it would seem one should include the $p^0$ explicitly.

Where do we go from here? Conclude PS (2.54) is incorrect?

It arises if one constructs QFT by causal +ve energy Poincare representations. One needs an integration measure over the +ve energy mass shell of the form
$$
\int\! d^4p \; \delta(p^2-m^2) \; \Theta(p_0)
$$
except that some constant factors are needed in order to end up with the usual 3D integral formulas and covariant commutation relations. Scharf also talks about integrals of this form -- which are closely related to all the stuff we've been talking about here.

Ok, all I know was the PS introduced the $\sqrt{2E_p}$ factor to make things Lorentz invariant. Is this what you are talking about?

 

[vanhees71]

But your solution to the first problem cannot be completely right. If you enclose no poles, the result is 0.

Note that you must close the contour in the upper $z$ half-plane. So for contour 1 you get 0, because in that case there are no poles inside the contour (contrary to what strangerep said in his question). If you close the contour in the lower half-plane the exponential blows up along the semi circle there!

In the second case both poles are within the contour, and then you have according to the residue theorem (I take $a>0$ to make the notation simple)
$$\int_{\mathcal{C}_w} \mathrm{d} z \frac{\exp(\mathrm{i} z k)}{k^2-a^2}=2 \pi \mathrm{i} \left [\frac{\exp(\mathrm{i} k a)}{2a}-\frac{\exp(-\mathrm{i} k a)}{2 a} \right ]=-\frac{2 \pi}{a} \sin(k a).$$
So here you have a factor 2 wrong.

The other cases you should do carefully in the same way. I must say, I do not understand the idea behind your calculations at all.

Now to Peskin-Schroeder (2.54). I'm always very sceptical about formulae in this book, because it's full of typos and little misconceptions. So it's always good to check his stuff. To check Eq. (2.54) we only have to do the $p^0$ integral at the very end, for $t=x^0-y^0>0$:
$$f(\vec{p},m)=-\int_{\mathrm{C}_{\text{PS}}} \frac{\mathrm{d} p^0}{2 \pi \mathrm{i}} \frac{\exp(-\mathrm{i} p^0 t)}{p^2-m^2}.$$
Now we have to close the contour in the lower half-plane (note the additional minus sign in the exponential compared to the integral before). Now the contour is clockwise and we have to take into account an additional sign in the residue theorem, which gives (since again we enclose both poles and $E_{\vec{p}}=+\sqrt{\vec{p}^2+m^2}$):
$$f(\vec{p},m)=+ \left [\frac{\exp(-\mathrm i E_{\vec{p}}t)}{2 E_{\vec{p}}}-\frac{\exp(+\mathrm{i} E_{\vec{p}}t)}{2 E_{\vec{p}}} \right ]=-\frac{\mathrm{i}}{E_{\vec{p}}} \sin(E_{\vec{p}} t).$$
But this is identical to the line before in Peskin/Schroeder. This is indeed also identical with one further line up since you come to it by substituting $\vec{p} \rightarrow -\vec{p}$ in the second part of the $\vec{p}$ integral. So in this case PS is correct.

 

[ianhoolihan]

But your solution to the first problem cannot be completely right. If you enclose no poles, the result is 0.

Note that you must close the contour in the upper $z$ half-plane. So for contour 1 you get 0, because in that case there are no poles inside the contour (contrary to what strangerep said in his question). If you close the contour in the lower half-plane the exponential blows up along the semi circle there!

In the second case both poles are within the contour, and then you have according to the residue theorem (I take $a>0$ to make the notation simple)
$$\int_{\mathcal{C}_w} \mathrm{d} z \frac{\exp(\mathrm{i} z k)}{k^2-a^2}=2 \pi \mathrm{i} \left [\frac{\exp(\mathrm{i} k a)}{2a}-\frac{\exp(-\mathrm{i} k a)}{2 a} \right ]=-\frac{2 \pi}{a} \sin(k a).$$
So here you have a factor 2 wrong.

The other cases you should do carefully in the same way. I must say, I do not understand the idea behind your calculations at all.

Now to Peskin-Schroeder (2.54). I'm always very sceptical about formulae in this book, because it's full of typos and little misconceptions. So it's always good to check his stuff. To check Eq. (2.54) we only have to do the $p^0$ integral at the very end, for $t=x^0-y^0>0$:
$$f(\vec{p},m)=-\int_{\mathrm{C}_{\text{PS}}} \frac{\mathrm{d} p^0}{2 \pi \mathrm{i}} \frac{\exp(-\mathrm{i} p^0 t)}{p^2-m^2}.$$
Now we have to close the contour in the lower half-plane (note the additional minus sign in the exponential compared to the integral before). Now the contour is clockwise and we have to take into account an additional sign in the residue theorem, which gives (since again we enclose both poles and $E_{\vec{p}}=+\sqrt{\vec{p}^2+m^2}$):
$$f(\vec{p},m)=+ \left [\frac{\exp(-\mathrm i E_{\vec{p}}t)}{2 E_{\vec{p}}}-\frac{\exp(+\mathrm{i} E_{\vec{p}}t)}{2 E_{\vec{p}}} \right ]=-\frac{\mathrm{i}}{E_{\vec{p}}} \sin(E_{\vec{p}} t).$$
But this is identical to the line before in Peskin/Schroeder. This is indeed also identical with one further line up since you come to it by substituting $\vec{p} \rightarrow -\vec{p}$ in the second part of the $\vec{p}$ integral. So in this case PS is correct.

I don't have time to make a full comment right now, and will expand on this later. However, it seems you have ignored the fact that the poles like on the real axis, as discussed intially by strangerep in post #3.

Cheers.

 

[ianhoolihan]

vanhees71, I should clarify that we were attempting to find the (real) integral $\int dp^0$. Yes, in the first case, the contour includes no poles, so by the residue theorem, the integral around the contour is zero. But that's not what we're trying to find --- we only want the part along the real axis.

 

[qbert]

vanhees71, I should clarify that we were attempting to find the (real) integral $\int dp^0$. Yes, in the first case, the contour includes no poles, so by the residue theorem, the integral around the contour is zero. But that's not what we're trying to find --- we only want the part along the real axis.

and that's where you're going wrong. the part along the real axis of the integral is undefined.
so, what we do is we tell you how to fix that, by giving a pole prescription
(a path that skirts the poles). what you're calculating is the principal value integral. this
is NOT what p&s tells you to calculate, so of course you're getting different answers.

 

[ianhoolihan]

and that's where you're going wrong. the part along the real axis of the integral is undefined.
so, what we do is we tell you how to fix that, by giving a pole prescription
(a path that skirts the poles). what you're calculating is the principal value integral. this
is NOT what p&s tells you to calculate, so of course you're getting different answers.

Ah, that makes things a little clearer! So, it should not really be
$$\int \frac{dp^0 }{2\pi i}\frac{-1}{p^2 - m^2}e^{-ip\cdot (x-y)}$$
but
$$\int_C \frac{dz }{2\pi i}\frac{-1}{z^2 - E_p^2}e^{-iz(x^0-y^0) -i\mathbf{p\cdot (x-y)}}$$
where $C$ is the contour given. Actually, as far as I'm aware $C$ could be any (anticlockwise) contour that surrounds both poles (for retarded propagator), as by the residue theorem, the result is the same. The contour could even be a circle around the poles, and only crosses the real axis, but does not lie upon it.

Anyway, I think strangerep and I are correct if it is an integral along the real axis (yes, I discussed that it was only the principal value, and strangrep indicated this was the same as the usual integral in this case). Otherwise, I agree with you if it is not an integral along the real axis, but one along the contour $C$.

Another point to mention: the principal value is (clearly) the same regardless of the four possible contours (i.e. Feynman = advanced = retarded propagators). So it must require the contour specific prescription you advise.

Cheers

 

[qbert]

exactly right.

you have to specify the contour for the principal value too.
it is: integrate up to pole - ε, integrate from pole + ε, up --
then take limit as ε goes to 0. which has the advantage
of never leaving the real axis, but the disadvantage of
being 1 a broken path, and 2 defined in terms of a limiting
operation.

but let me repeat the integral along the real axis is undefined
until you give a pole prescription. as a real integral it is
undefined as written. there is no "usual integral" in this case,
you have to figure out some way to handle the poles.

 

[ianhoolihan]

exactly right.

you have to specify the contour for the principal value too.
it is: integrate up to pole - ε, integrate from pole + ε, up --
then take limit as ε goes to 0. which has the advantage
of never leaving the real axis, but the disadvantage of
being 1 a broken path, and 2 defined in terms of a limiting
operation.

but let me repeat the integral along the real axis is undefined
until you give a pole prescription. as a real integral it is
undefined as written. there is no "usual integral" in this case,
you have to figure out some way to handle the poles.

Sorry, I edited that post with the comment about it being any possible contour $C$ --- do you agree with this?

You don't really need to specify the contour for the principal value --- by definition, it is the one you described, in the same way the contour for a real integral is along the real axis.

I admit that the principal value integral didn't sit well with me. However, strangerep implies that in this case the principal value was the same (post #10, point 7). If this is true, then I am fine with this --- do you agree it is true?

Lastly, am I right in saying that the point of the complex integration is simply to shorten the formula? PS give the non-complex formula in (2.54), but it can be shortened with the complex integral. In this sense, I take back my prior statement that the propagator "depends" on the contour chosen --- the propagators themselves are different due to how they are derived etc, and it just turns out that these different formulae can be written in the same form, but with complex integrals and specific different contours.

 

[qbert]

1. you DO have to specify a path for the principal value -
it's the one i mentioned with SYMMETRIC limits. you
don't have to think about it AS a path - but it is.
otherwise the integral is UNDEFINED. So when you
say it's that one "by definition", what do you think
the "definition" is for?

2. there is no USUAL integral in this case. Lebesgue or not.

3. The point of the complex integration is to tell you how
to define an undefined integral. You can think about it
as a clarifying statement. writing $\int_{-\infty}^\infty$ doesn't mean anything
in this case. The contour tells you what ∫ means.

4. P&S want to write the integral as a space-time integral,
so in one sense they're just rewriting.
But at every point it's a well defined integral. As they go from
the second to the last line to the last
when they write the dp⁰ integral they HAVE to tell
you which contour to pick. that's why they have the whole
paragraph after 2.54 explaining how they're writing the
integral and give a pole prescription.

-----------------------------

as to point 1.
consider
$$\int_{-\infty}^\infty \frac{e^{-|x|}}{x} dx$$
with the symmetric definition you get
$$\text{p.v.}\int_{-\infty}^\infty \frac{e^{-|x|}}{x} dx = 0,$$
But suppose we defined instead
$$\text{p.v.}'\int_{-\infty}^\infty \frac{e^{-|x|}}{x} dx = \lim_{\epsilon \rightarrow 0} \left( \int_{-\infty}^{-\epsilon/2} \frac{e^{-|x|}}{x} \,dx + \int_{\epsilon}^\infty \frac{ e^{-|x|}}{x} \, dx \right),$$
with a small amount of work this can be shown to give
$$\text{p.v.}'\int_{-\infty}^\infty \frac{e^{-|x|}}{x} dx = \ln(2).$$

 

[ianhoolihan]

1. you DO have to specify a path for the principal value -
it's the one i mentioned with SYMMETRIC limits. you
don't have to think about it AS a path - but it is.
otherwise the integral is UNDEFINED. So when you
say it's that one "by definition", what do you think
the "definition" is for?

2. there is no USUAL integral in this case. Lebesgue or not.

3. The point of the complex integration is to tell you how
to define an undefined integral. You can think about it
as a clarifying statement. writing $\int_{-\infty}^\infty$ doesn't mean anything
in this case. The contour tells you what ∫ means.

4. P&S want to write the integral as a space-time integral,
so in one sense they're just rewriting.
But at every point it's a well defined integral. As they go from
the second to the last line to the last
when they write the dp⁰ integral they HAVE to tell
you which contour to pick. that's why they have the whole
paragraph after 2.54 explaining how they're writing the
integral and give a pole prescription.

1. OK, I assumed a symmetric limit was part and parcel of principal value: http://mathworld.wolfram.com/CauchyPrincipalValue.html. I guess you have to specify about which point you are taking the limit though.

2. OK.

3/4. OK, I agree that they couldn't write
$$\int^\infty_{-\infty}\frac{dp^0}{2\pi i} \frac{-1}{p^2-m^2}e^{-ip\cdot(x-y)}$$
without explaining that contour integration is required. However, why is that specific contour required? Would it not be the same to use any other anticlockwise contour containing the poles? It gives (symbolically) the same answer, by the residue theorem, does it not?

 

[vanhees71]

This is exactly what I don't like with Peskin Schroeder! First he writes some sloppy undefined integral and then pulls some contour magic out of the hat. To the contrary the important point is not to find the integrand of the Fourier transform, which is quite simple algebra, but to derive the correct contour from the beginning.

In vacuum qft, what you usually have to calculate in perturbation theory, is the time-ordered propagator, which is defined for a Klein-Gordan field, by the vacuum-expectation value
$$\mathrm{i} \Delta_c(x,y)=\langle \Omega | \mathcal{T}_c \hat{\phi}(x) \hat{\phi}^{\dagger}(y) | \Omega \rangle.$$
Then you write out the time-ordering symbol with Heaviside-unitstep functions, and those precisely tell you how you have to choose your path to circumvent the poles in the $p^0$-Fourier integral.

You find many details about these issues in my writeup on Green's functions for relativistic many-body theory in the real-time Schwinger-Keldysh formalism:

http://fias.uni-frankfurt.de/~hees/publ/green.pdf

 

[strangerep]

Note that you must close the contour in the upper $z$ half-plane. So for contour 1 you get 0, because in that case there are no poles inside the contour (contrary to what strangerep said in his question).

Sorry, the numerator in the integrand should have been $e^{-ikz}$ (or else specified instead that $k<0$).

But [ianhoolihan's] solution to the first problem cannot be completely right. If you enclose no poles, the result is 0.

That's only true if the total contribution from the small detouring semicircles around the real poles is zero. In the partial solutions so far, that has not been proven.

 

[ianhoolihan]

This is exactly what I don't like with Peskin Schroeder! First he writes some sloppy undefined integral and then pulls some contour magic out of the hat. To the contrary the important point is not to find the integrand of the Fourier transform, which is quite simple algebra, but to derive the correct contour from the beginning.

In vacuum qft, what you usually have to calculate in perturbation theory, is the time-ordered propagator, which is defined for a Klein-Gordan field, by the vacuum-expectation value
$$\mathrm{i} \Delta_c(x,y)=\langle \Omega | \mathcal{T}_c \hat{\phi}(x) \hat{\phi}^{\dagger}(y) | \Omega \rangle.$$
Then you write out the time-ordering symbol with Heaviside-unitstep functions, and those precisely tell you how you have to choose your path to circumvent the poles in the $p^0$-Fourier integral.

You find many details about these issues in my writeup on Green's functions for relativistic many-body theory in the real-time Schwinger-Keldysh formalism:

http://fias.uni-frankfurt.de/~hees/publ/green.pdf

I'm glad someone else finds PS a little fishy sometimes. To be honest, I'm working through PS as it the usual basis for courses (including those that I'll be taking this year), and not because I think it is well written. Hopefully I'll gain the main ideas, and then can progress to Weinberg...

I had a brief skim over the pdf you linked, but at this stage, it's a little too far beyond me!

Sorry, the numerator in the integrand should have been $e^{-ikz}$ (or else specified instead that $k<0$).

I picked that up a while after I'd posted the solutions too. Don't think it changes things.

That's only true if the total contribution from the small detouring semicircles around the real poles is zero. In the partial solutions so far, that has not been proven.

I think what's been said is that we are not trying to find the integral in the limit of smaller semicircles. That is the path, and they are meant to be of finite radius. (I'm still waiting to hear if they can be any anticlockwise contour surrounding the poles.) Hence, the residue theorem works fine.

 

[strangerep]

Regarding the point about defining the integral correctly... of course we intend
the Cauchy principal value interpretation of the integral. I.e., the ill-defined integral
$$
I_1 ~:=~ \int_{-\infty}^{+\infty} \!\! dx \; \frac{e^{-ikx}}{x^2 - a^2}
$$
is tacitly interpreted as
$$
\def\eps{\epsilon}
I_1 ~:=~ P.V. \int_{-\infty}^{+\infty} \!\! dx \; \frac{e^{-ikx}}{x^2 - a^2}
~\equiv~
\lim_{\eps\to 0} \left(\,
\int_{-\infty}^{-a-\eps}\!\!\!\!\dots
~+~ \int_{-a+\eps}^{a-\eps} \!\!\!\!\dots
~+~ \int_{a+\eps}^{+\infty}\!\!\!\!\dots \;\right) ~,
$$
to be performed by contour integration in the complex $x$-plane.
Cf. http://en.wikipedia.org/wiki/Cauchy_principal_value

Any use of such complex energies, etc, is only a technical device, since complex
energies (in this context, at least) are unphysical. To be physically useful, the
result for $I_1$ must not depend on which technical device we choose.
The Cauchy PV interpretation, combined with contour integration satisfies
this criterion, since it doesn't matter which way we choose to form a closed
contour (provided the total contour integral exists, of course, and that any extra
detours in the complex plane are accounted for when isolating the
contribution from $I_1$ which is what we want).

 

[strangerep]

I'm glad someone else finds PS a little fishy sometimes.

Do you have a copy of the errata list for your edition of PS? They can be found at:
http://www.slac.stanford.edu/~mpeskin/QFT.html

 

[ianhoolihan]

Regarding the point about defining the integral correctly... of course we intend
the Cauchy principal value interpretation of the integral. I.e., the ill-defined integral
$$
I_1 ~:=~ \int_{-\infty}^{+\infty} \!\! dx \; \frac{e^{-ikx}}{x^2 - a^2}
$$
is tacitly interpreted as
$$
\def\eps{\epsilon}
I_1 ~:=~ P.V. \int_{-\infty}^{+\infty} \!\! dx \; \frac{e^{-ikx}}{x^2 - a^2}
~\equiv~
\lim_{\eps\to 0} \left(\,
\int_{-\infty}^{-a-\eps}\!\!\!\!\dots
~+~ \int_{-a+\eps}^{a-\eps} \!\!\!\!\dots
~+~ \int_{a+\eps}^{+\infty}\!\!\!\!\dots \;\right) ~,
$$
to be performed by contour integration in the complex $x$-plane.
Cf. http://en.wikipedia.org/wiki/Cauchy_principal_value

Any use of such complex energies, etc, is only a technical device, since complex
energies (in this context, at least) are unphysical. To be physically useful, the
result for $I_1$ must not depend on which technical device we choose.
The Cauchy PV interpretation, combined with contour integration satisfies
this criterion, since it doesn't matter which way we choose to form a closed
contour (provided the total contour integral exists, of course, and that any extra
detours in the complex plane are accounted for when isolating the
contribution from $I_1$ which is what we want).

OK, I'm getting confused by the opposing views presented, but I think posts #23 and #24 clarify things. The principal value approach would be correct if attempting to evaluate along the real axis (principal value is and is not (?) the same as the real integral, from what I've been told). However, PS are not talking of this integral. They are talking of $\int_C$ where $C$ is the given (or possibly more general) contour around the poles.

strangerep, thanks for the list of errata --- most useful!

 

[strangerep]

In the second case both poles are within the contour, and then you have according to the residue theorem (I take $a>0$ to make the notation simple)
$$\int_{\mathcal{C}_w} \mathrm{d} z \frac{\exp(\mathrm{i} z k)}{k^2-a^2}=2 \pi \mathrm{i} \left [\frac{\exp(\mathrm{i} k a)}{2a}-\frac{\exp(-\mathrm{i} k a)}{2 a} \right ]=-\frac{2 \pi}{a} \sin(k a).$$
So here you have a factor 2 wrong.

Your second expression is the same as
$$\frac{\pi i}{a} \Big( e^{ika} - e^{-ika} \Big)$$
which is the same as Ian's result (except for a minus sign at the front which I think is due to the different contour orientations). But I don't see a "factor of 2" error here. (?)