- #1
geoduck
- 258
- 2
Just out of curiosity, why doesn't
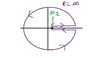
[tex]\int_{1}^{\infty} dx \sqrt{x-1} \mbox{ }e^{-x^4} [/tex]
vanish by contour integration?
The contour starts just above the real x-axis at x=1, goes rightward to x=infinity, then counter-clockwise from 0 to 2pi, then it goes leftward back to x=1.
Since the integrand has no poles, the entire integral should be zero. Along the real axis, the leftward and rightward contributions are equal. At infinity the contributions are zero. So it seems that the entire integral should be zero.
This is absurd of course, but I can't figure out where I went wrong in my logic.
[tex]\int_{1}^{\infty} dx \sqrt{x-1} \mbox{ }e^{-x^4} [/tex]
vanish by contour integration?
The contour starts just above the real x-axis at x=1, goes rightward to x=infinity, then counter-clockwise from 0 to 2pi, then it goes leftward back to x=1.
Since the integrand has no poles, the entire integral should be zero. Along the real axis, the leftward and rightward contributions are equal. At infinity the contributions are zero. So it seems that the entire integral should be zero.
This is absurd of course, but I can't figure out where I went wrong in my logic.