Leo Liu
- 353
- 156
Hi I am back :).
I have been doing some Simulink modeling for a project. I modeled it with a discrete system due to the controller rate. I have noticed that for all the discrete system I have tried, adding a derivative filter not only improves the performance (smaller settling time), but it is sometimes also necessary.
The following example involving a discrete PID and a 2nd order discrete transfer function illustrates the behaviour:
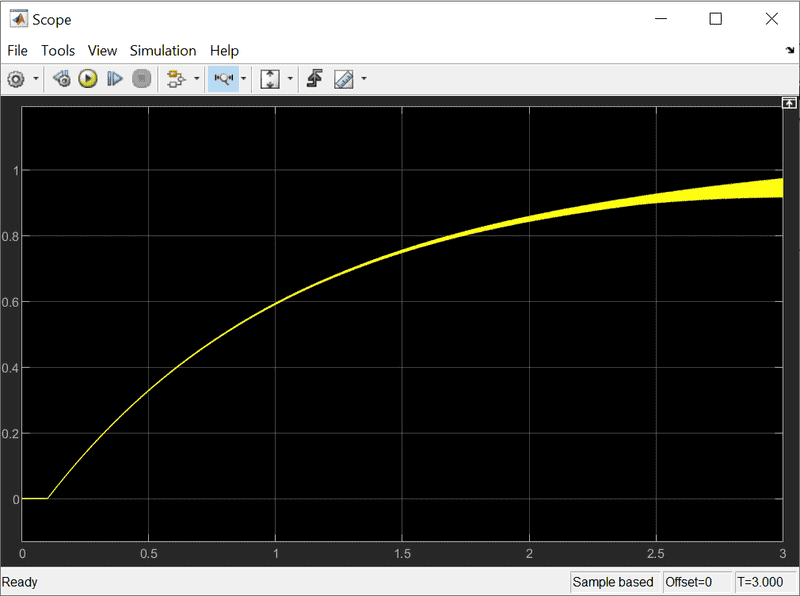
Autotune with no derivative filter N:
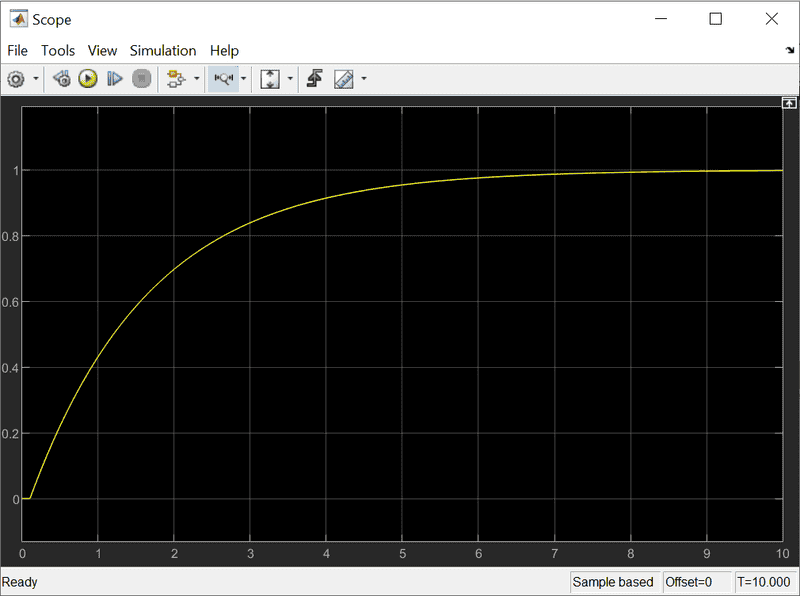
Autotune with derivative filter N:
I was wondering why such a behaviour would occur. Also, should I model the transfer function as discrete or continuous system for a physical system like F=ma? Any input will be appreciated.
I have been doing some Simulink modeling for a project. I modeled it with a discrete system due to the controller rate. I have noticed that for all the discrete system I have tried, adding a derivative filter not only improves the performance (smaller settling time), but it is sometimes also necessary.
The following example involving a discrete PID and a 2nd order discrete transfer function illustrates the behaviour:
Autotune with no derivative filter N:
Autotune with derivative filter N:
I was wondering why such a behaviour would occur. Also, should I model the transfer function as discrete or continuous system for a physical system like F=ma? Any input will be appreciated.