- #1
Xforce
- 73
- 6
As most people know, massive stars such as blue giant of Wolf-Rayet stars are short lived,only for a few million years.well tiny stars such as red dwarfs seems to be immortal by human’s prospective, and indeed they can live up to a trillion years! Most people thought it was only caused by the huge fuel consumption of the massive stars. But it turns out small stars have a convection between the outer layer and the core,and all the hydrogen in the star can be used as fuel. Stars more massive than 0.5 solar masses have a radiation zone, where radiation passes by.
In a medium sized star like sun, the convection zone is between the core and the surface and the core is a radiation zone. The convection zone is away from the core, means that the hydrogen between the surface and core can not be used as fuel. In a planetary nebula there is a lot of hydrogen. In a massive star, the convection zone is in the core and the radiation zone is between surface and core. Because large stars (more than 8 solar masses)can fuse multiple elements until iron-56, so the fuel in the core should be convected from the inner core and outer core. But turns out there are still layers of different elements in a dying core of a large star. Why is this happening and why stars with different masses have different structures?
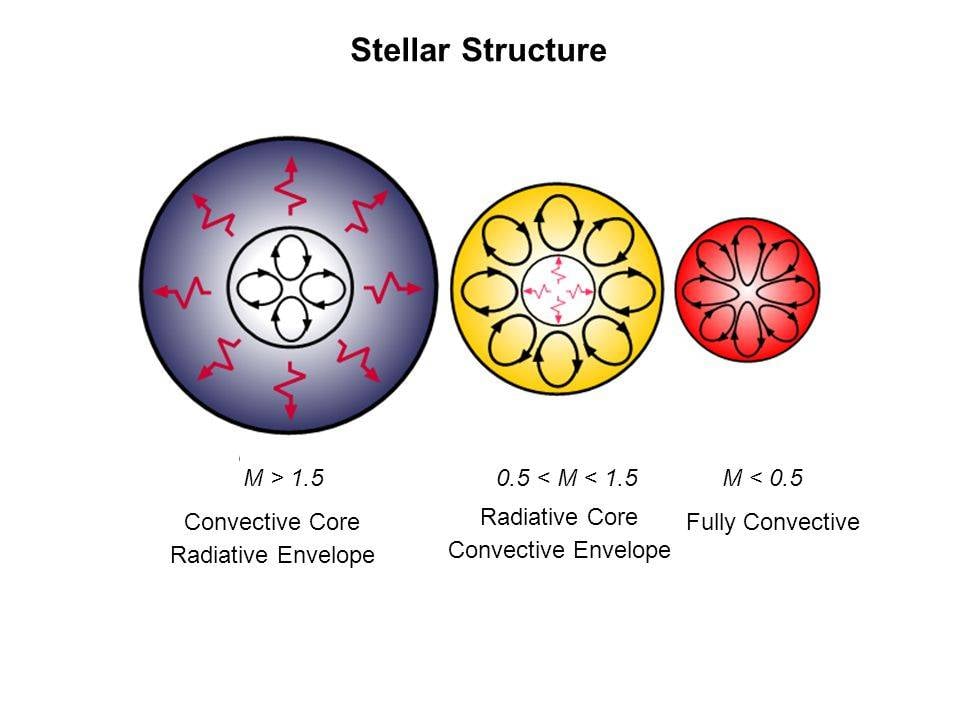
In a medium sized star like sun, the convection zone is between the core and the surface and the core is a radiation zone. The convection zone is away from the core, means that the hydrogen between the surface and core can not be used as fuel. In a planetary nebula there is a lot of hydrogen. In a massive star, the convection zone is in the core and the radiation zone is between surface and core. Because large stars (more than 8 solar masses)can fuse multiple elements until iron-56, so the fuel in the core should be convected from the inner core and outer core. But turns out there are still layers of different elements in a dying core of a large star. Why is this happening and why stars with different masses have different structures?
