Converting between field operators and harmonic oscillators

[SupernerdSven]

TL;DR Summary

I am trying to convert an expression written in terms of field operators and derivatives to be written in terms of ladder operators, but one expression seems to be Hermitian while the other isn't, so something is wrong.

Suppose we have a Hamiltonian containing a term of the form

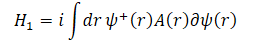
where ∂=d/dr and A(r) is a real function. I would like to study this with harmonic oscillator ladder operators. The naïve approach is to use

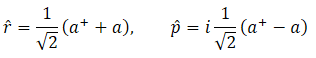
where I have set ħ=1 so that

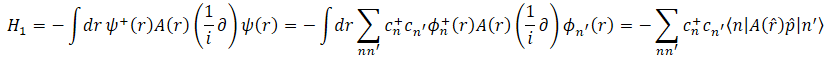
This term is Hermitian because r and p both are.*

However, if we check for Hermicity in real space, we realize that

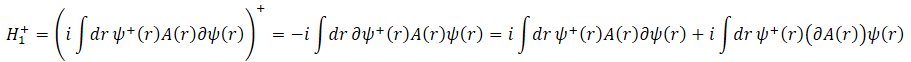
We integrated by parts in the third step. This is *not* Hermitian; it has an extra term.

What is the cause of this disagreement, and what is the proper way to study this Hamiltonian using the ladder operators?

----------

(Note: The actual Hamiltonian term I have is

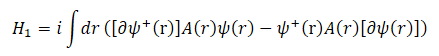
which *is* Hermitian, but it suffers from a similar problem when expressed in the conventional form with all derivatives on ψ(r). In that case, an extra non-Hermitian term appears.)

----------

*Edit:
Thank you to HomogeneousCow for pointing out the sloppiness of my notation which treated the position representation of momentum as if it were the general operator. While correcting this sloppy notation I realized that my error was in the section marked with an asterisk. Clearly

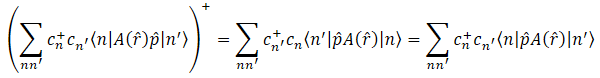
is not Hermitian. Lesson learned, sloppy notation leads to careless mistakes.

 

[HomogenousCow]

I'm still reading your post, but it seems like there are some severe typos in the second equation as it makes no sense as it stands.

I expressed $H_1$ in the momentum basis and it is indeed non-Hermitian. Define the decomposition
$$\psi(x) = \int \frac{dk}{2\pi} a_k ~e^{ikx}$$ it follows that $$i\int dx A(x) \psi(x)^\dagger \frac{d}{dx} \psi(x) = - \int \frac{dk}{2\pi}\frac{dp}{2\pi} k ~\tilde A(p-k) a^{\dagger}_p~a_k$$ which is not hermitian. I don't want to be condescending but from your working it doesn't seem like you fully understand how the field operator formalism works, for example your third line of equation has position space functions and derivatives on the RHS which is supposed to be in a non-spatial basis.

 

[SupernerdSven]

Thank you for pointing out my abuse of notation, in treating the general momentum operator and its real-space representation as the same. I had been thinking of the derivative as the momentum operator. When editing the question to fix my notation, I realized my error. I have edited the question both to fix the and to make a note about the resolution.