Convolution - calculation and drawing

[aruwin]

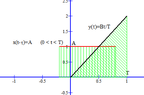
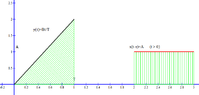
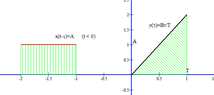
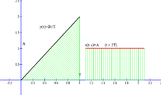
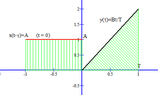
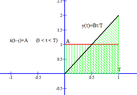
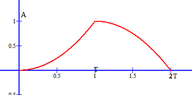
Hi! I need your help with convolution. I am having problem understanding it. I don't understand the example, it shows the calculation and the drawing. Could you please explain the solution to me - why the ranges of t are taken that way and how does the drawing represent the answer?I'll show you one example, and one exercise (the one I need to solve).


Ignore the Japanese writing, it only says to "find z", and "when t=..."

 

[BAdhi]

I will try to explain the convolution by analyzing it graphically. (you can see how convolution happen in this link http://upload.wikimedia.org/wikipedia/commons/b/b9/Convolution_of_spiky_function_with_box2.gif)

The convolution is $z(t)= \int \limits_{-\infty}^{\infty} y(\tau)x(t-\tau) \;d\tau$

now take

[math] y(\tau) = \frac{B\tau}{T} \quad 0\leq \tau \leq T[/math]

[math] x(\tau) = A \quad 0\leq \tau\leq T \implies x(t-\tau) = A \quad t-T\leq \tau \leq t[/math]

above two function are shown in the below graph (remember the variable of the integral is $\tau$)View attachment 3428

Now we should see what happens to the integral ($z(t)$) when the value $t$ changes

(i) when $t\leq 0$

As the graph below suggest there is no overlapping in the $x(t-\tau)$ and $y(\tau)$
View attachment 3429View attachment 3431

Therefore $\int_{-\infty}^\infty x(t-\tau)y(\tau)$ is 0. Thus when $t\leq 0 \implies z(t)=0$

(ii) When $0<t\leq \tau$
View attachment 3427
View attachment 3433

As the graph shows the overlapping of two graphs starts at $\tau=0$ and ends at $\tau=t$.

Therefore the convolution at this scenario will be,

$z(t) = \int_0^t x(t-\tau)y(\tau) d\tau=\int_0^t A\frac{B}{T}\tau d\tau$

Thus, when $$0<t\leq T \implies z(t) = \int_0^t A\frac{B}{T}\tau d\tau$$

(iii) when $T<t\leq 2T$View attachment 3434

View attachment 3432

As the graphs show the overlapping always end at $T$ and starts at $t-T$. Therefore the limits of the convolution in this scenario changes as following

$\int\limits_{t-T}^{T} x(t-\tau)y(\tau) \;d\tau = \int\limits_{t-T}^T A\frac{B}{T}\tau d\tau$

$$\therefore \text{when } T<t\leq 2T \implies z(t)=\int\limits_{t-T}^T A\frac{B}{T}\tau d\tau$$

(iv) when $t>2T$

View attachment 3430

On this occasion also the overlapping does not occur (similar to t<0). Therefore the convolution is zero.

Thus $t>2T \implies z(t) =0$So eventually the piece-wise function of the z will be as following.

$$z(t)=\begin{cases}0 \quad t\leq 0 \\ A\frac{B}{2T}t^2 \quad 0<t\leq T \\ \frac{AB}{2T}(2tT-t^2)\quad T<t\leq 2T\\0 \quad t>2T \\ \end{cases}$$

View attachment 3436

Hope this will help to understand the convolution theory :)

 

[aruwin]

I will try to explain the convolution by analyzing it graphically. (you can see how convolution happen in this link http://upload.wikimedia.org/wikipedia/commons/b/b9/Convolution_of_spiky_function_with_box2.gif)

The convolution is $z(t)= \int \limits_{-\infty}^{\infty} y(\tau)x(t-\tau) \;d\tau$

now take

[math] y(\tau) = \frac{B\tau}{T} \quad 0\leq \tau \leq T[/math]

[math] x(\tau) = A \quad 0\leq \tau\leq T \implies x(t-\tau) = A \quad t-T\leq \tau \leq t[/math]

above two function are shown in the below graph (remember the variable of the integral is $\tau$)View attachment 3428

Now we should see what happens to the integral ($z(t)$) when the value $t$ changes

(i) when $t\leq 0$

As the graph below suggest there is no overlapping in the $x(t-\tau)$ and $y(\tau)$
View attachment 3429View attachment 3431

Therefore $\int_{-\infty}^\infty x(t-\tau)y(\tau)$ is 0. Thus when $t\leq 0 \implies z(t)=0$

(ii) When $0<t\leq \tau$
View attachment 3427
View attachment 3433

As the graph shows the overlapping of two graphs starts at $\tau=0$ and ends at $\tau=t$.

Therefore the convolution at this scenario will be,

$z(t) = \int_0^t x(t-\tau)y(\tau) d\tau=\int_0^t A\frac{B}{T}\tau d\tau$

Thus, when $$0<t\leq T \implies z(t) = \int_0^t A\frac{B}{T}\tau d\tau$$

(iii) when $T<t\leq 2T$View attachment 3434

View attachment 3432

As the graphs show the overlapping always end at $T$ and starts at $t-T$. Therefore the limits of the convolution in this scenario changes as following

$\int\limits_{t-T}^{T} x(t-\tau)y(\tau) \;d\tau = \int\limits_{t-T}^T A\frac{B}{T}\tau d\tau$

$$\therefore \text{when } T<t\leq 2T \implies z(t)=\int\limits_{t-T}^T A\frac{B}{T}\tau d\tau$$

(iv) when $t>2T$

View attachment 3430

On this occasion also the overlapping does not occur (similar to t<0). Therefore the convolution is zero.

Thus $t>2T \implies z(t) =0$So eventually the piece-wise function of the z will be as following.

$$z(t)=\begin{cases}0 \quad t\leq 0 \\ A\frac{B}{2T}t^2 \quad 0<t\leq T \\ \frac{AB}{2T}(2tT-t^2)\quad T<t\leq 2T\\0 \quad t>2T \\ \end{cases}$$

View attachment 3436

Hope this will help to understand the convolution theory :)

Thank you for the explanation. But I still don't understand how you get the amplitude? How do you know the values of the y axis?

 

[aruwin]

I will try to explain the convolution by analyzing it graphically. (you can see how convolution happen in this link http://upload.wikimedia.org/wikipedia/commons/b/b9/Convolution_of_spiky_function_with_box2.gif)

The convolution is $z(t)= \int \limits_{-\infty}^{\infty} y(\tau)x(t-\tau) \;d\tau$

now take

[math] y(\tau) = \frac{B\tau}{T} \quad 0\leq \tau \leq T[/math]

[math] x(\tau) = A \quad 0\leq \tau\leq T \implies x(t-\tau) = A \quad t-T\leq \tau \leq t[/math]

above two function are shown in the below graph (remember the variable of the integral is $\tau$)View attachment 3428

Now we should see what happens to the integral ($z(t)$) when the value $t$ changes

(i) when $t\leq 0$

As the graph below suggest there is no overlapping in the $x(t-\tau)$ and $y(\tau)$
View attachment 3429View attachment 3431

Therefore $\int_{-\infty}^\infty x(t-\tau)y(\tau)$ is 0. Thus when $t\leq 0 \implies z(t)=0$

(ii) When $0<t\leq \tau$
View attachment 3427
View attachment 3433

As the graph shows the overlapping of two graphs starts at $\tau=0$ and ends at $\tau=t$.

Therefore the convolution at this scenario will be,

$z(t) = \int_0^t x(t-\tau)y(\tau) d\tau=\int_0^t A\frac{B}{T}\tau d\tau$

Thus, when $$0<t\leq T \implies z(t) = \int_0^t A\frac{B}{T}\tau d\tau$$

(iii) when $T<t\leq 2T$View attachment 3434

View attachment 3432

As the graphs show the overlapping always end at $T$ and starts at $t-T$. Therefore the limits of the convolution in this scenario changes as following

$\int\limits_{t-T}^{T} x(t-\tau)y(\tau) \;d\tau = \int\limits_{t-T}^T A\frac{B}{T}\tau d\tau$

$$\therefore \text{when } T<t\leq 2T \implies z(t)=\int\limits_{t-T}^T A\frac{B}{T}\tau d\tau$$

(iv) when $t>2T$

View attachment 3430

On this occasion also the overlapping does not occur (similar to t<0). Therefore the convolution is zero.

Thus $t>2T \implies z(t) =0$So eventually the piece-wise function of the z will be as following.

$$z(t)=\begin{cases}0 \quad t\leq 0 \\ A\frac{B}{2T}t^2 \quad 0<t\leq T \\ \frac{AB}{2T}(2tT-t^2)\quad T<t\leq 2T\\0 \quad t>2T \\ \end{cases}$$

View attachment 3436

Hope this will help to understand the convolution theory :)

But you got the shapes the other way around. It's x(tau)y(t-tau).