Coordinate transformation of the Navier Stokes equation

[hcpysicist]

Homework Statement

Given navier stokes equation in certisian form ,it is asked to use coordinate transformation equation to derive navier stokes equation in cylindrical coordinates .

Relevant Equations

x=rcos(theta),
y=rsin(theta)
z=z

i have successfully transformed the continuity equation using coordinate transform,but having trouble with the momentum equation .

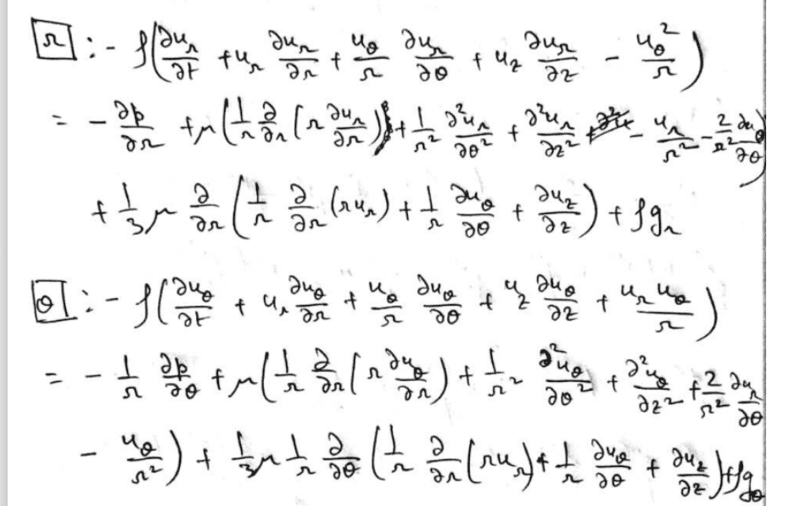
can someone kindly provide the transformation of the right hand sight of equation of the image i have attached.