Coordinates of a point on a rotating wheel

[realanswers]

Homework Statement

A mass m is fixed to a given point on the rim of a wheel of radius R that rolls without
slipping on the ground. The wheel is massless, except for a mass M located at its
center. Find the equation of motion for the angle through which the wheel rolls. For
the case where the wheel undergoes small oscillations, find the frequency.

Relevant Equations

L = T - V
$$x = R \theta - \sin \theta$$
$$y = R - \cos \theta$$

My issue is in deriving the coordinates of a point on a wheel that rotates without slipping. In Morin's solution he says that:

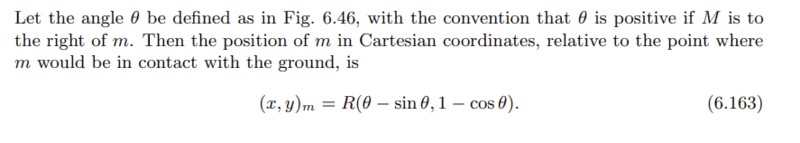
My attempt at rederiving his equation:

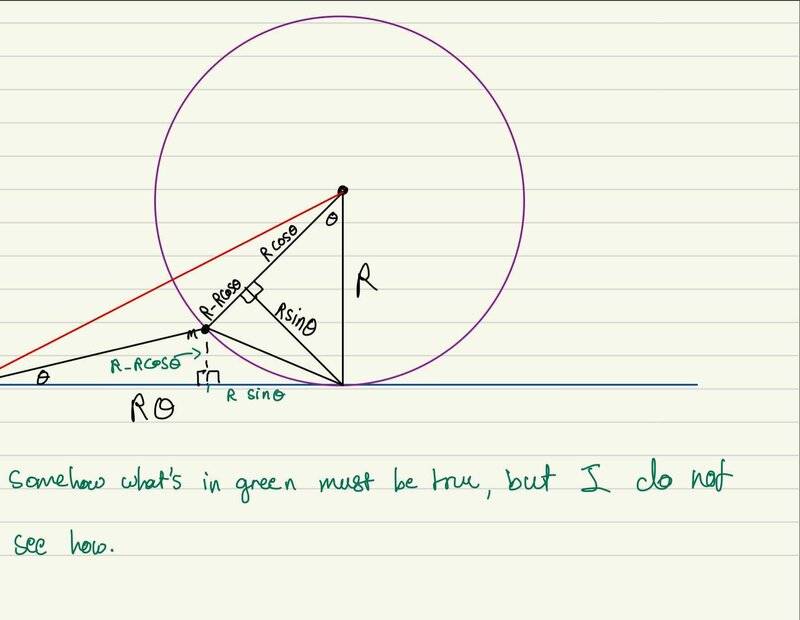
I do not understand how the triangle on the bottom with sides indicated in green is the same as the triangle on top that is the only way I can get morin's solution. Am I missing something? This doesn't seem like a trivial thing (unless I am approaching it incorrectly and there is an easier way of seeing it).

 

[anuttarasammyak]

Please find attached the figure I draw on your sketch, which I interpreted from the text. The circle in orange rolls on x axis to become the circle in purple.

https://www.physicsforums.com/attachments/320402

 

[kuruman]

The easy way to derive the EoM is to forget Morin's triangles and do it in two quick steps.
(a) Write an equation for a point on the rim in a frame of reference moving at the same velocity $\vec v$ with the wheel. Taking the origin of coordinates to be at the point of contact at $t=0$,
$y=R(1- \cos\omega t)~$;$~~x=-R\sin \omega t$.
(b) Transform to the rest frame of the surface on which the wheel is rolling by adding $vt$ in the direction of motion. Then the position vector of the point of interest is
$\vec r= v t~\hat x -R\sin \omega t~\hat x+R(1- \cos\omega t)~\hat y.$

With $\theta =\omega t$ and $v=\omega R$ for rolling without slipping, one gets
$$\vec r=R \theta~\hat x -R\sin \theta~\hat x+R(1- \cos\theta)~\hat y= R(1-\sin\theta)~\hat x+R(1- \cos\theta)~\hat y$$which is Morin's expression. I find this method straightforward and easy to derive whenever needed.

 

[haruspex]

how the triangle on the bottom with sides indicated in green is the same as the triangle on top

Label the points
O centre of circle
C point of contact with ground below O
P mass on circumference
Drop perpendicular from P to meet OC at Q.
Can you see that PQC is congruent to both of the small triangles?