Corollary 8: Integration in 'Polar Coordinates'

[LightKage]

I am reading Spivak's Differential Geometry Vol. 1. I am stuck for some days in chapter 8 about integrating forms on manifolds. Maybe someone can clear my doubt.

First, I will 'type' what the corollary says:

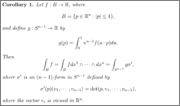
My doubt is regarding this affirmation:

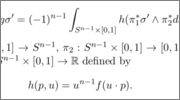
The book it says is easy to see. Well I think the (-1)^n-1, does not exist. I worked in the n=2 case just to see where I was doing an error, but still I have that negative sign does not exist.

I will post my working out:

http://postimg.org/image/ghfrg9jq1/

I believe Fubini is justified. A good person that was trying to help me, said that instead of Fubini, I can only interchange the integrals adding the (-1)^n-1 term, but I don't know why.

Any help is appreciated,

thanks

Sergio

 

[jvicens]

Dear Sergio,

Thank you for reaching out for help with your doubt about integrating forms on manifolds in Spivak's Differential Geometry Vol. 1. I understand that you have been stuck on this topic for a few days and are looking for clarification on the corollary mentioned in chapter 8.

In order to help you better, I would first like to clarify the affirmation that you are having doubts about. From what I understand, you are questioning the existence of the term (-1)n-1 in the corollary. I would like to assure you that this term does indeed exist and is an important factor in the integration of forms on manifolds.

To understand why this term exists, it is important to understand the concept of orientation on a manifold. Orientation refers to the direction in which a curve or surface is traversed, and it plays a crucial role in integration of forms. In the n=2 case, as you have worked out, the negative sign may seem to not exist because you are considering only one orientation. However, in higher dimensions, it becomes necessary to consider both orientations.

Fubini's theorem is indeed justified in this case, but as your friend mentioned, you may also interchange the integrals by adding the term (-1)n-1. This is because when you interchange the integrals, the orientation of the manifold changes, and the term (-1)n-1 takes into account this change in orientation.

I hope this helps to clear your doubt. If you still have any further questions or need more clarification, please do not hesitate to ask. Keep up the good work in studying Spivak's Differential Geometry and best of luck with your studies!