Correct approach in resolving a force into its different components

[Nova_Chr0n0]

Homework Statement

The force F = 450 lb acts on the frame. Resolve this force into components acting along members AB and AC, and determine the magnitude of each component. (Figure is attached below)

Relevant Equations

N/A

I've already got the answer and the way to solve it (parallelogram), but I'm just wondering why I cannot use the technique I've learned in the lesson torque.

Let's focus on the line AB, if I use what I've learned in torque, the components would be like this:

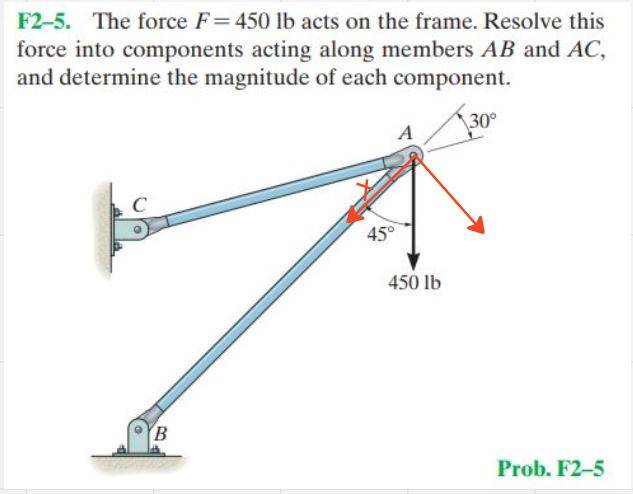
To find the force component in AB, I could just solve my assign variable "x" and use trigonometry. In this scenario I would have
x = AB = 450cos(45)

But this answer is incorrect and is not similar to when I use the parallelogram method. My question is, what is the difference between them? Is the technique only for torque/moment problems?

 

[TSny]

There can be confusion about the meaning of "component" here.

To "resolve $\vec F$ into components acting along AB and AC" means to find a vector parallel to AB and a vector parallel to AC such that the two vectors add to produce $\vec F$.

To "find the component of $\vec F$ along AB" can mean to project $\vec F$ along the line AB and this is different than the previous meaning of "component". This component would be $450 \cos(45^0)$ lb, as you calculated. If you draw a sketch where you project $\vec F$ along AB and also project $\vec F$ along AC, you should be able to see that these "components" do not add to produce $\vec F$.

 

[Nova_Chr0n0]

There can be confusion about the meaning of "component" here.

To "resolve $\vec F$ into components acting along AB and AC" means to find a vector parallel to AB and a vector parallel to AC such that the two vectors add to produce $\vec F$.

To "find the component of $\vec F$ along AB" can mean to project $\vec F$ along the line AB and this is different than the previous meaning of "component". This component would be $450 \cos(45^0)$ lb, as you calculated. If you draw a sketch where you project $\vec F$ along AB and also project $\vec F$ along AC, you should be able to see that these "components" do not add to produce $\vec F$.

Now I understand it much better. Thanks for the explanation!

 

[Lnewqban]

... I've already got the answer and the way to solve it (parallelogram), but I'm just wondering why I cannot use the technique I've learned in the lesson torque.

Because, if member AB were horizontal, no force would be transferred through it onto the point B.
Applying what you have learned about torque to such frame, would reveal that certain horizontal force and its corresponding reaction would be acting on point B.

Considering the frame as a solid that is anchored to pivots B and C is actually the proper way to calculate the internal forces in members AB and AC (which can only be oriented along each member as compression or tension).

 

[jbriggs444]

To find the force component in AB, I could just solve my assign variable "x" and use trigonometry. In this scenario I would have
x = AB = 450cos(45)

But this answer is incorrect and is not similar to when I use the parallelogram method. My question is, what is the difference between them? Is the technique only for torque/moment problems?

If I understand the concern, the problem is that here you are being asked to break a vector into components using a "basis" that is not "orthonormal".

Ordinarily we choose a coordinate system so that coordinate axes are perpendicular. This makes things nice so that when you take the dot product of two vectors, you can consider each component independently of the others: $\vec{(x_1, y_1, z_1)} \cdot \vec{(x_2, y_2, z_2)} = x_1x_2 + y_1y_2 + z_1z_2$

It also makes things nice when it comes to calculating torques. We can write the vector cross product in component form with some formulas that I will not write down.

You can recognize that a coordinate system is not "orthonormal" when the dot product of the unit vector along one coordinate axis and the unit vector along another coordinate axis is non-zero.

The above discussion would be dealt with more systematically in "linear algebra" where you would learn about vector spaces and inner product spaces.