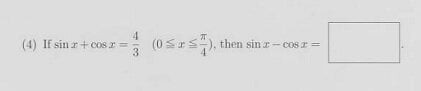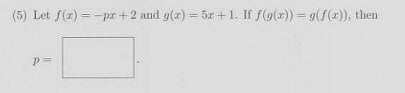- #1
squexy
- 18
- 0
´
Could anyone tell me if the resolutions of these questions are correct?View attachment 3754
Cosx = 4/3 - sin x
Six - 4/3 - Sin x = 0
2 Sinx = 4/3
Sinx = 4/6
Cosx = 4/3 - 4/6
Cosx = 8/6 - 4/6
Cosx = 4/6
View attachment 3755
G(x) = 5x + 1
5*(px+2)+1
5px + p = 5px + 10+ 1
p = 11
Could anyone tell me if the resolutions of these questions are correct?View attachment 3754
Cosx = 4/3 - sin x
Six - 4/3 - Sin x = 0
2 Sinx = 4/3
Sinx = 4/6
Cosx = 4/3 - 4/6
Cosx = 8/6 - 4/6
Cosx = 4/6
View attachment 3755
G(x) = 5x + 1
5*(px+2)+1
5px + p = 5px + 10+ 1
p = 11