Thermofox
- 144
- 26
- Homework Statement
- ##0.5## moles of an ideal gas, at ##P_1= 1atm## and ##T_1= 20 °C##, go through the following cycle:
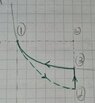
From 1 to 2: irreversible adiabatic;
From 2 to 3: reversible isovolumetric;
From 3 to 1: reversible isothermic.
In this cycle the system absorbs ##Q_h=890J## and ##V_2 = 3V_1##
- Relevant Equations
- ##\Delta U = W + Q##
I need to determine:
1)##\Delta S## of the system
2)Total work done by the system
3)##\Delta S## of the surroundings
For point 1 ##\Delta S_{system}=0## because it is a cyclic process.
For point 2 ##W_{net}= W_{1-2} + W_{2-3} + W_{3-1}##.
Since 2-3 is an isovolumetric process, ##W_{2-3}=0##
=> ##W_{1-2}= \Delta U= nc_v\Delta T_{1-2}## and ##W_{3-1}= -ln(\frac {V_1} {V_3})##.
I'm not sure about point 3 though. Because surely ##\Delta S_{1-2}^{surr.}= 0## since in the process there is no heat exchange between system and surroundings. But I don't know how to determine the change for the other 2 transformations. I assume I should be using ##Q_h##, that in this case must be all absorbed during 2-3, but still I don't know how to proceed forward.
1)##\Delta S## of the system
2)Total work done by the system
3)##\Delta S## of the surroundings
For point 1 ##\Delta S_{system}=0## because it is a cyclic process.
For point 2 ##W_{net}= W_{1-2} + W_{2-3} + W_{3-1}##.
Since 2-3 is an isovolumetric process, ##W_{2-3}=0##
=> ##W_{1-2}= \Delta U= nc_v\Delta T_{1-2}## and ##W_{3-1}= -ln(\frac {V_1} {V_3})##.
I'm not sure about point 3 though. Because surely ##\Delta S_{1-2}^{surr.}= 0## since in the process there is no heat exchange between system and surroundings. But I don't know how to determine the change for the other 2 transformations. I assume I should be using ##Q_h##, that in this case must be all absorbed during 2-3, but still I don't know how to proceed forward.