Could spacetime be non-orientable?

[Jarek 31]

TL;DR Summary

(Why) Can we be certain that spacetime is orientable?

Einstein's general relativity theory assumes that spacetime is a manifold with intrinsic curvature proportional to stress-energy tensor.
But manifolds, in principle, can be non-orientable, like Möbius strip or Klein bottle:

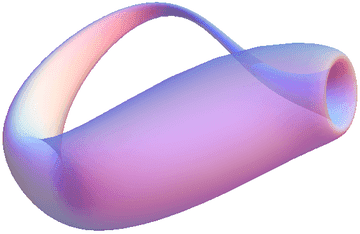
So could spacetime be non-orientable?
If not, is that because of impossibility of getting such stress-energy tensor configuration, or are there some other reasons?
If yes, could e.g. traveling through such Klein-bottle-like wormhole perform P or T symmetry on such object?

I have found 3 peer-reviewed articles optimistic about such possibility (should they be so?):
Nonorientable spacetime tunneling: https://journals.aps.org/prd/abstract/10.1103/PhysRevD.59.064026
Observing other universes through ringholes and Klein-bottle holes: https://aip.scitation.org/doi/abs/10.1063/1.4734422?download=true&journalCode=apc
The orientability of spacetime: https://iopscience.iop.org/article/10.1088/0264-9381/19/17/308

 

[martinbn]

These( orientability and stress energy tensor) are unrelated.

 

[Jarek 31]

My point was that non-orientable manifolds might require some characteristic configurations of intrinsic curvature - e.g. Gauss-Bonnet ( https://en.wikipedia.org/wiki/Gauss–Bonnet_theorem ) allows to get genus by integrating curvature.
Are there this kind of theorems for orientability? Parallel transport through both paths should give opposite vector ... For external curvatures there should be, I am not certain about intrinsic?
Mobius strip can be realized with zero Gaussian curvature, but it has boundary ... Klein bottle might be realizable with zero curvature in higher dimensions (?)

 

[stevendaryl]

I don’t think that General Relativity assumes that spacetime is orientable. The theory works fine for any topology.

 

[Jarek 31]

Indeed, general relativity alone doesn't seem to have any conflict with non-orientability (?)
However, there might be other issues - e.g. a rocket traveling through such Klein-bottle-like wormhole, should have applied P or T symmetry:

1) P symmetry would e.g. transform life into its mirror version ( https://en.wikipedia.org/wiki/Mirror_life ) ... and matter into mirror matter ( https://en.wikipedia.org/wiki/Mirror_matter ) - which would be a bit different if P symmetry is indeed violated by standard model (in contrast to CPT).

2) T symmetry is more problematic - would switch past and future light cones - e.g. scrambling an egg inside such rocket, would be "unscrambling" for an external observer - would 2nd law of thermodynamics work in the opposite direction there? (a related question: if our Universe would finally undergo Big Crunch, shouldn't it have entropy similar to Big Bang?)

ps. Dozens of peer-reviewed articles about mirror particles, universe etc.: https://people.zeelandnet.nl/smitra/mirror.htm

 

[robphy]

To add to @stevendaryl 's post, the key requirement for a spacetime is a Lorentz-signature metric that is sufficiently smooth. To satisfy the field equations, one has to have a stress-energy tensor that is equal to the Einstein curvature tensor.

It seems to me that the "physical problem" has more to do with whether the associated stress-energy is "physically reasonable" (subject to, say, "energy conditions", a well-posed "initial value problem", and possibly some "causality conditions").

Possibly interesting reading:
"Global structure of spacetimes" by Geroch and Horowitz
in "General relativity: An Einstein centenary survey" edited by Hawking and Israel, 1979.

 

[pervect]

I recollect reading about time orientable manifolds in the context of GR, which implies that there could be such things as non-time orientable manifolds. It was probably in some discussion of the causal structure of space-time, where time-orientability was a pre-requisite assumption to the discussion.

 

[Jarek 31]

Indeed non-time orientabilitiy is more problematic and interesting case than space.
A rocket flying through such wormhole would have switched past and future light cones, e.g. egg scrambled there would be "unscrambled" for an external observer, laser would use stimulated absorption ... 2nd law of thermodynamics would go backward inside.

It is great thought experiment to remind that thermodynamics is in fact time-symmetric: for example having two connected compartment with all gas molecules being in one of them, it would have tendency for entropy growth if evolving in both time directions.
So what about entropy of hypothetical Big Crunch - as it depends on densities and energies, shouldn't it be similar as in Big Bang?

 

[PeterDonis]

non-time orientabilitiy is more problematic and interesting case than space.

These aren't two different things. We are talking about spacetime; there is no invariant way to separate spacetime into "space" and "time". So there are not two types of possible non-orientability here. There is only one.

A rocket flying through such wormhole

What does a wormhole have to do with non-orientability?

would have switched past and future light cones

Where are you getting this from?

thermodynamics is in fact time-symmetric: for example having two connected compartment with all gas molecules being in one of them, it would have tendency for entropy growth if evolving in both time directions.

You are misstating this. The correct statement is that, if the system is in a microstate that does not correspond to thermal equilibrium, but you don't know which particular microstate it is in, then the second law predicts entropy increase in both directions of time. Or, to put it another way, the second law predicts that that state that is not in thermal equilibrium was caused by a random fluctuation of the system--that it was in thermal equilibrium in the past and will be in thermal equilibrium again in the future.

However, if you know exactly which microstate the system is in, thermodynamics does not necessarily predict entropy increase in both directions. For example, if the microstate is a particular microstate of our universe, say a billion years ago, thermodynamics predicts entropy increase in the forward direction of time, but entropy decrease in the backward direction of time--because that particular microstate is known to be one that originated, not from a random fluctuation out of thermal equilibrium, but from an initial condition, the Big Bang, that had even lower entropy.

Also, none of this has anything to do with lack of orientability.

what about entropy of hypothetical Big Crunch - as it depends on densities and energies, shouldn't it be similar as in Big Bang?

No, because the microstate of a Big Crunch, if there were to be one (our best current models say there won't be in our actual universe) will not be identical to the microstate of the Big Bang. The Big Bang microstate was extremely smooth and homogeneous. The Big Crunch microstate will be extremely gravitationally clumped. In the presence of gravity, the latter microstate has far higher entropy than the former.

 

[Jarek 31]

Please take a look at the mentioned literature to get deeper answers to your questions.
For Riemannian manifolds all directions are indeed equivalent, but for pseudo-Riemnannian spacetime signature is what "separates" time and space.
Non-orientability would mean existence of path such that parallel transport through it would invert a vector - the literature distinguish time and space nonorientability corresponding to T or P symmetry (applied to objects traveling such path) - are you saying that T and P symmetry can be unified?
Klein-bottle-like wormhole is the simplest way to imagine spacetime non-orientability, but maybe there are also other ways (?) - https://iopscience.iop.org/article/10.1088/0264-9381/19/17/308 mentions "Gibbons and Herdeiro make similar observations for a particle traversing their supersymmetric rotating black hole."

Regarding entropy growth, I have written "having two connected compartment with all gas molecules being in one of them, it would have tendency for entropy growth if evolving in both time directions." - as in diagram in the middle below.
Knowing only that there is such situation, and evolving or trying to predict what is before or after, entropy should grow - it has combinatorial tendency to get p=1/2 particles on the left, as such number of combinations binomial(n,pn) ~ exp(n h(p)) grows faster than for different p.

Regarding the difference between Big Bang and Big Crunch, finally everything is hypothesized to be "gravitationally clumped" in a single point - how situation in a single point could distinguish these two scenarios?

 

[PeterDonis]

for pseudo-Riemnannian spacetime signature is what "separates" time and space.

Signature means there are three different types of intervals--timelike, spacelike, and null--instead of just one (spacelike). But that, in itself, does not give any invariant way to separate time and space. It just means there are three different types of intervals.

Non-orientability would mean existence of path such that parallel transport through it would invert a vector

Yes.

the literature distinguish time and space nonorientability corresponding to T or P symmetry

The literature certainly talks about T and P symmetry, but that's not the same thing as non-orientability as you just defined it (what I responded "yes" to just now). There are plenty of spacetime geometries with T and/or P symmetry that are orientable in the sense you defined.

Regarding entropy growth,

This is a separate topic and should be discussed in a separate thread.

 

[PeterDonis]

Please take a look at the mentioned literature to get deeper answers to your questions.

They're all paywalled. Do you have links to the arxiv preprints?

 

[Jarek 31]

Yes.

So imagine a rocket travels through such path inverting a vector - if it is spatial vector applying P symmetry (e.g. of life into https://en.wikipedia.org/wiki/Mirror_life ), if it is temporal vector applying T symmetry (e.g. egg scrambling -> "unscrambling", entropy growth -> decrease).

Searching titles of these articles: https://arxiv.org/abs/gr-qc/9901016 https://arxiv.org/abs/1102.3784 https://arxiv.org/pdf/gr-qc/0202031.pdf

 

[PeterDonis]

So imagine a rocket travels through such path inverting a vector - if it is spatial vector applying P symmetry (e.g. of life into https://en.wikipedia.org/wiki/Mirror_life ), if it is temporal vector applying T symmetry (e.g. egg scrambling -> "unscrambling", entropy growth -> decrease).

No. You are still confusing P and T symmetry of the spacetime with non-orientability. For example, non-orientability leading to closed timelike curves is not the same as the spacetime being time symmetric.

Searching titles of these articles: https://arxiv.org/abs/gr-qc/9901016 https://arxiv.org/abs/1102.3784 https://arxiv.org/pdf/gr-qc/0202031.pdf

Got them, will take a look.

 

[Jarek 31]

Non-orientability means existence of path such that going through it, some vector is inverted - how does it differ from applying P or T symmetry?

 

[PeterDonis]

Non-orientability means existence of path such that going through it, some vector is inverted

More precisely, it means that the "handedness" of a set of 4 orthonormal vectors--one timelike and three spacelike--gets reversed. There are not two different ways this can happen; there is only one. "Inverting" the timelike vector is equivalent to "inverting" any of the spacelike vectors--all of those operations invert the handedness of the set of 4 orthonormal vectors, which is the "orientation" of spacetime.

how does it differ from applying P or T symmetry?

Because the P and T symmetry transformations are local; you apply them at a single point of spacetime (or to all points in a region). But the reversal of "handedness" that happens with non-orientability is global--it happens after the set of 4 orthonormal vectors has traveled along a particular path that goes through a non-orientable region. That's a different operation.

 

[Jarek 31]

So imagine a rocket travels through such vector-inverting path and e.g. returns to Earth ... would there be any effect on its crew?

 

[PeterDonis]

imagine a rocket travels through such vector-inverting path and e.g. returns to Earth ... would there be any effect on its crew?

I would think that the internal "handedness" of their bodies, for things which are not symmetrical, would be reversed--for example, their hearts and the internal arrangements of blood vessels leading to and from the heart (and similarly for other internal organs).

However, I have not actually seen a detailed attempt to model this mathematically.

 

[Jarek 31]

The symmetry you are referring to is P, and change would go down to molecules e.g. L-sugars instead of D-sugars ( https://en.wikipedia.org/wiki/Mirror_life ) ... and matter https://en.wikipedia.org/wiki/Mirror_matter

However, what if the inverted vector would be in temporal direction?

 

[vanhees71]

I've not followed the entire discussion, but isn't it very difficult to decide about the large-scale structure of spacetime by observation? The point of GR is that it deals with local properties, i.e., all we observe are local observables. Concerning the large-scale structure we extrapolate these local observations of far distant events (and this means of events both far away and long ago) to what happened at this past and distant events by using some models. E.g., in cosmology we use the FLRM metric to describe the spacetime (averaged over large enough spacetime regions) and a model of the "matter content" based on observations like the fluctuations of the cosmic microwave background and redshift-distance relations from Supernovae observations. I'm not so sure that we can find observables distinguishing between different global spacetime models and particularly decide whether it's orientable or not.

 

[Jarek 31]

Indeed it would be great to be able to find some experimental evidence:
- for P symmetry (assuming it is violated by particle physics), here are dozens of papers about such hypothetical mirror matter: https://people.zeelandnet.nl/smitra/mirror.htm
- for T symmetry, I would say that inside such rocket from our perspective e.g. eggs would "unscramble", laser would use stimulated absorption, entropy would decrease ... but how to test it in astronomical observations? Maybe "mirror star" absorbing more light than emitting? or https://en.wikipedia.org/wiki/White_hole obtained by black hole going through such wormhole?

 

[stevendaryl]

Signature means there are three different types of intervals--timelike, spacelike, and null--instead of just one (spacelike). But that, in itself, does not give any invariant way to separate time and space. It just means there are three different types of intervals.

The issue is about the direction of timelike vectors. In Minkowsky spacetime, it is possible to choose a consistent definition of “future-pointing” for all timelike vectors. In a spacetime that is not orientable in time, there is no consistent continuous way to do this.

 

[stevendaryl]

The intuitive description from Wikipedia is this:

If a 4D spacetime is space-orientable, then

whenever two right-handed observers head off in rocket ships starting at the same spacetime point, and then meet again at another point, they remain right-handed with respect to one another.

If a 4D spacetime is time-orientable, then

then the two observers will always agree on the direction of time at both points of their meeting

To make these distinctions, you don't need a universal definition of time and space, only a universal definition of timelike and spacelike.

 

[Jarek 31]

In Minkowsky spacetime, it is possible to choose a consistent definition of “future-pointing” for all timelike vectors. In a spacetime that is not orientable in time, there is no consistent continuous way to do this.

Indeed, the natural intuition of clear distinction of past and future lightcones might not necessarily be true - reminding e.g. that "proofs" of entropy growth in time/CPT symmetric models (e.g. https://en.wikipedia.org/wiki/H-theorem ) always require some approximation (mean-field, called Stosszahlansatz) - applying this symmetry before, we would "prove" tendency for entropy growth in opposite time direction.

 

[PeterDonis]

what if the inverted vector would be in temporal direction?

I'm not sure the figure you've drawn is actually possible (it appears to have two possible worldlines with the same 4-velocity emerging from the same point, which is self-contradictory), but there are known solutions in GR with closed timelike curves, such as Godel spacetime, which amounts to the same thing geometrically. Note that Godel spacetime's underlying manifold is $R^4$, so no Klein bottle-type manifold is even required to have closed timelike curves in GR.

However, the implications for things like entropy are not quite what you describe:

I would say that inside such rocket from our perspective e.g. eggs would "unscramble", laser would use stimulated absorption, entropy would decrease

No, what would happen is that such time-asymmetric processes as eggs scrambling would not even be possible in the first place in such a spacetime, because they would have to go both ways at once along the same worldline.

Godel spacetime, for example, is stationary, including the matter in it--which means that the matter in it cannot undergo any kind of time asymmetric change at all.

 

[vanhees71]

Then it's of course an interesting question, how to formally exclude such solutions of the Einstein equations as "unphysical". In other words, what forbids solutions like Gödel's universe?

Also the Kerr solution, describing a rotating black hole, has closed time-like curves. Is there any chance to observe them?

 

[Jarek 31]

The diagram is visualization of inverting temporal vector while traveling through nonorientable e.g. Klein-bottle-like wormohole.
Sure, it requires spacetime being embedded in something higher dimensional (e.g. https://en.wikipedia.org/wiki/Whitney_embedding_theorem ), and generally I don't see it very realistic - but in theory allowed by general relativity, hence it is worth to understand it, its consequences - what might lead to experimental verification (?)

So what would happen with rocket traveling through such hypothetical path and returning to Earth, its crew?

Sure spacetime should be stationary (Einstein's block universe, https://en.wikipedia.org/wiki/Eternalism_(philosophy_of_time) ), already resolving hypothetical temporal causal loops.

 

[PeterDonis]

The diagram is visualization of inverting temporal vector while traveling through nonorientable e.g. Klein-bottle-like wormohole.

Your diagram has the two lines coming together into one but "pointing in opposite directions". That can't happen. The object can only have one 4-velocity at any given point in spacetime; its worldline can't split or rejoin itself.

The usual visualization of a closed timelike curve is just a circle. It should be obvious that it is impossible to make a continuous choice of the "future" direction of the light cones in any region of spacetime that contains such a closed timelike curve--i.e., that such a region of spacetime cannot be time orientable. (IIRC this is proved formally as a theorem in Hawking & Ellis.) But the circle only has one tangent vector at each point, so it doesn't have the problem described above that your diagram does.

 

[PeterDonis]

in theory allowed by general relativity

A closed timelike curve that is a circle is allowed by GR. Your diagram as you drew it is not, for the reason I gave in my previous post just now.

what would happen with rocket traveling through such hypothetical path and returning to Earth, its crew?

First we need to know if it's even possible for that to happen at all. In other words, we need to know if GR permits a spacetime geometry with the following features:

(1) It has regions which are not time orientable (contain closed timelike curves) and other regions which are time orientable (so the Earth can be in such a region).

(2) It has to be possible for a timelike worldline to start in an orientable region, go into a non-orientable region, and then return back to the same orientable region from which it started (so the rocket can return back to Earth, where it came from).

I'm not aware of any solution of the Einstein Field Equation that has both these properties.

Godel spacetime violates property #1; the entirety of Godel spacetime is non-orientable (there are closed timelike curves through every point).

Kerr spacetime violates property #2; once you've entered the non-orientable region (near the ring singularity), you can't return back to the orientable region where you started (because you passed through an event horizon and you can't go back through it the other way).

I've looked through the papers that have been linked to (or the arxiv preprints, anyway), and none of them appear to address this issue.

 

[Jarek 31]

Just found two diagrams here: https://physics.stackexchange.com/q...of-the-standard-non-time-orientable-spacetime - maybe they are better?
If somebody believes in wormhole possibility, gluing them in non-orinatable way as in Klein bottle doesn't seem much more difficult (?)

 

[PeterDonis]

Just found two diagrams here

Diagrams by themselves aren't very helpful; there are lots of ways of drawing diagrams with light cones going every which way that don't correspond to any actual solution of the Einstein Field Equation.

The stackexchange thread you linked to references Wald, so I'll need to go look at Wald to see in what context the diagram given appears.

 

[PeterDonis]

Just found two diagrams here

Btw, the OP of the stack exchange thread is wrong when it says the diagrams it refers to are of the only non-time-orientable spacetime ever described "outside of de Sitter space with some identifications" (not sure what that refers to either). Godel spacetime, which I've already described in this thread, is another.

 

[stevendaryl]

Btw, the OP of the stack exchange thread is wrong when it says the diagrams it refers to are of the only non-time-orientable spacetime ever described "outside of de Sitter space with some identifications" (not sure what that refers to either). Godel spacetime, which I've already described in this thread, is another.

Being non-orientable isn’t exactly the same thing as having closed timelike curves. Having CTLCs means there is a timelike path leading back to the same point in spacetime. That by itself doesn’t preclude orientability. For example, consider a spacetime that is topologically a cylinder, with the direction “around” the cylinder being timelike. That’s got CTLCs, but it’s still orientable. You can consistently define timelike vectors as future-pointing or past-pointing.

 

[PeterDonis]

consider a spacetime that is topologically a cylinder, with the direction “around” the cylinder being timelike. That’s got CTLCs, but it’s still orientable. You can consistently define timelike vectors as future-pointing or past-pointing.

Yes, this is true, but note that this spacetime still violates property #2 described in my post #29, so it still can't serve as the basis for the OP's thought experiment.

 

[PeterDonis]

The stackexchange thread you linked to references Wald, so I'll need to go look at Wald to see in what context the diagram given appears.

The first diagram in post #30 is Fig. 8.1 in Wald, but it is only given as an informal example and is not discussed at all, nor is any actual description of such a spacetime in terms of equations (such as a metric) given. So there is no actual proof that there is a solution of the Einstein Field Equation that looks like the diagram.