yesmale4
- 41
- 1
- Homework Statement
- Three equal positive charges, q = 8.5 μC each, are arranged at the vertices of equilateral triangle (see figure below). A negative charge, Q, is placed at the center of the triangle such that all four charges are in equilibrium.
- Relevant Equations
- Ef=0
f=kq1q2/r^2
hello i would like to understand something, i found the right answer but there is still something i don't understand.
here is the figure
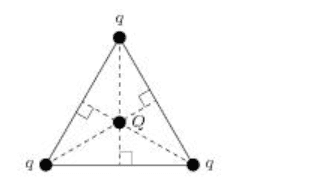
and here is my correct solution

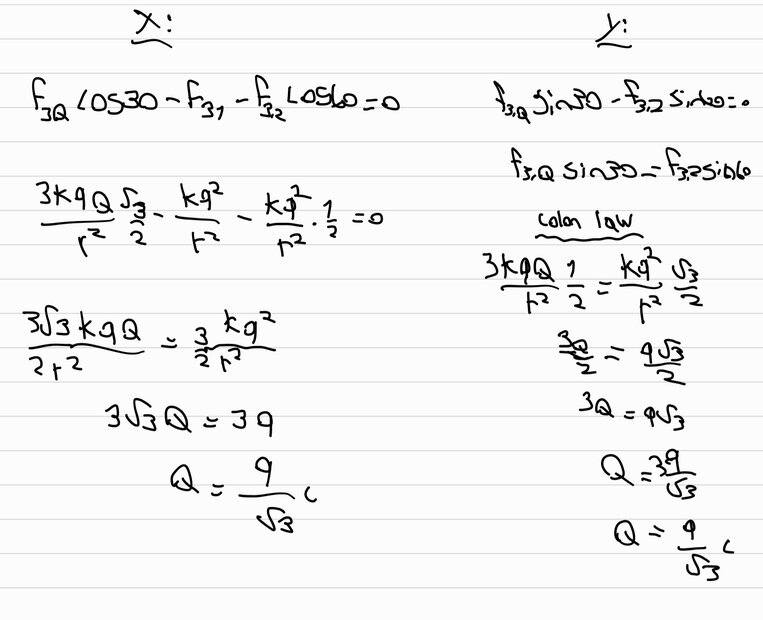
what i don't understand is why F(3,Q) is 3kQ/r^2
i mean why is the 3? i only calculat the force between q3 and Q so why the 3 before?
here is the figure
and here is my correct solution
what i don't understand is why F(3,Q) is 3kQ/r^2
i mean why is the 3? i only calculat the force between q3 and Q so why the 3 before?
Last edited: