Counteractive forces at 3 points

[Lead Foot]

K, so my name is Kris. New to the site. Not a physics major or anything. lol Had a question I was trying to figure out the answer too and now I am lost. It has to do with suspension, applied torque, and how that torque or force is multiplied depending on stationary points in relation to a rotating axle. I have some illistrations I can upload and try to explain what I am thinking.

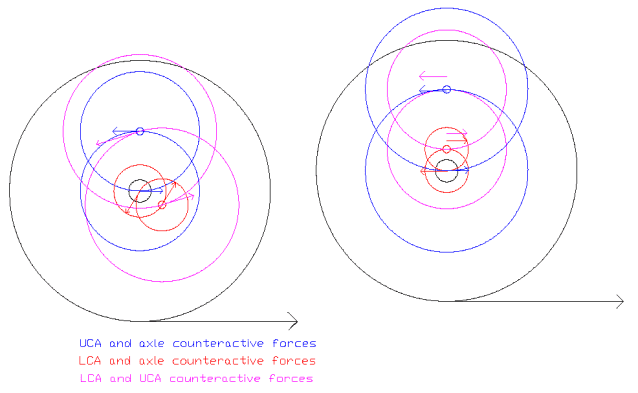
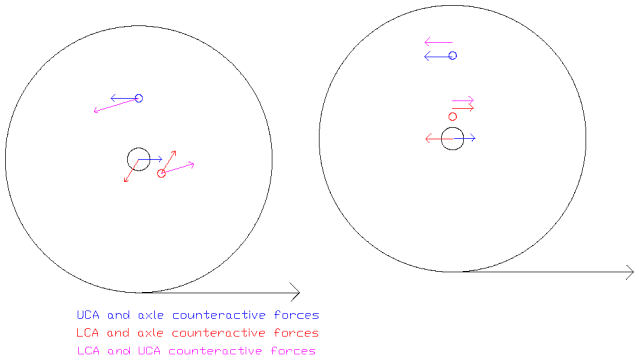
K so the blue and red circles are stationary points in a system. They are supposed to stop the center axle from rotating while braking or accellerating. The biggest black circle would be the tire. The arrows are showing how the forces are applied to each point under braking (if I did it right).

So My question is, if under acceleration the tires see 2000ft/lbs of torque. How much would each of these mounts see with the two different configurations? Is there a simple formula to find out how the force is multiplied?

 

[Lead Foot]

No one? Did I not state the situation and question good enough? Or is this in the wrong section?

 

[Lead Foot]

SO what's going on guys? I though you could help. Is that I sound to stupid to understand the answer to my own question? lol

 

[nvn]

Lead Foot: You did not yet state (1) the direction of travel of the vehicle, (2) whether the wheel is driven or passive, (3) whether the vehicle is accelerating or braking, (4) where the torque comes from and the direction of the torque.

 

[Lead Foot]

Vehicle traveling from right to left across the screen (so the front is at the left). I would like to know both accelerating and braking. Either way wouldn't there be a significant difference in acting forces from the left setup vs the setup on the right? The wheel of course is driven and the torque comes from the axle/tirepatch contact with the ground.

As you accelerate the wheel grabbing on the ground would cause the axle to want to rotate clockwise and opposite while braking. The arrows showing applied forces are while braking in the illistration.

 

[nvn]

Lead Foot: After I posted the above, I realized, I think you will not be able to determine how much of the torque is resisted by each of the two braking mechanisms unless you know the normal force applied by each mechanism, and the coefficient of friction of each mechanism.

 

[Lead Foot]

I don't think you understand my question... those 2 bolt holes I have drawn (the smallest red and blue circles in the illistration) are drilled through a plate mount that is welded to the 2.75" axle housing in a normal linked suspension setup. Those mounts are then attached to joints with a bolt then to a control arm and then then frame of the vehicle.

Like this basic drawing

Or this 3d drawing.

I realize that accelerating would probably be easier to calculate since brake pads and breaking forces are harder to calculate accurately.

So as far as torque applied to the axles and tires.

An inline6 puts out 235 foot pounds of torque max to the transmission. The transmission gear ratio in first gear is 2.8:1 sending 658 pounds of torque to the t case, which has a low range gear ratio of 2.72:1 multiplying the torque to 1789 then sending that to the differential and reducing another 4.88:1 for a total of 8734 foot pounds of torque to the back axle. The axle housing is 2.75" diameter and the tires are 35" diameter.

Is that enough information?

 

[nvn]

Lead Foot: Post 7 is starting to make your question more clear. You said this wheel travels from right to left. Therefore, your wheel shown in the first picture of post 7 is a front wheel, correct? And as you said, we are now talking about only acceleration, not braking. Therefore, your vehicle shown in the first picture of post 7 is accelerating to the left.

There is not a simple formula. You will need to have a good background in drawing dimensioned free-body diagrams, statics, and some dynamics. The axle torque passes directly to the wheel, and to the ground, with probably little being lost to the wheel bearings. You can assume the wheel bearing friction is zero. Therefore, I think the friction force on the tire (which equals the horizontal applied force on the axle housing) is Fo = [T - (I*ax/ro)]/ro, where T = axle drive torque, I = wheel mass moment of inertia, ax = vehicle acceleration, and ro = wheel radius.

You are missing a coil spring. It is required to hold your axle housing in place. Once you add that, then you will need the exact x and y coordinates of the strut bolt locations, and of the coil spring location. You will also need the exact angle of each of these three components.

The horizontal applied force on your axle housing is Fo. The vertical applied force is N, which is the vertical force applied by the road on the tire. (There is a slight amount of rolling resistance, but I am neglecting it.) Then, you have three equilibrium equations, and three unknowns. The unknowns are the axial force in strut 1, strut 2, and the coil spring. After you solve for these three unknown axial forces, you can compute the forces on each weld.

You can do the above twice, once for each of your two strut configurations, and then compare the forces and moments on the axle housing brackets and welds for each configuration.

 

[Ranger Mike]

Almost there, people. Post 5 shows a typical transfer/ differential design to transfer rotary power of the engine to the pavement. I have a problem with the design in post 5. The differential is suspended with two equal length trailing arms (ok so far) and a top link to handle the twist when the horsepower is applied.
There are two glaring problems. 1. the location of the differential is offset to one side. This is typically done to improve the torque transfer. A Rear Wheel Drive vehicle will have a short right rear axle and longer left rear axle. The stubby axle is stronger as it is on the side most frequently where power is applied. Rt. rear is the drive side in 1,2,3 forward gears, The left rear it the drive side when the car is in reverse gear.
2. The top link should be over the right rear and not the left rear side. See example in my post below). Normal production RWD cars had right side bias due to diff offset. If you think about what's going on, when power is applied, the tires hook up and the diff. wants to twist around the mounting points..the trailing arms are ok but the top link is mounted on the long spindly axle tube way far away from where the action is..and on the wrong side of the diff. ( for forward gear scenario)
Depending upon the engine output, that is a lot of torque being applied to the long axle tube. Mounting the top link closer to the diff. center housing and on the right side will impact traction a lot.

One final thought. The torque calculations discussed are static. The true dynamics get very hairy when you start looking at what happens when nth power is applied. The left rear of the car moves up and the right rear digs in and there is a considerably more load on the right rear side of the vehicle due to this lateral weight transfer. We have not even discussed the front to rear weight transfer which is huge..but that's another discussion.

 

[Ranger Mike]

one more thing..the total torque calculation to the wheels is prob correct..the percentage of this total to each wheel must take into account the length of the axles..diff with 50 - 50 mounting location will deliver equal amount of torque to each wheel (static calculation)
from memory the top link should be mounted at the center mass of the car otherwise the tire loading will not be equal under acceleration. this gets confusing when we are talking about a race car that has more left side weight. Example- if the car has 60 inch rear track width and 58 percent left side weight so center of mass is ; 60 x .58=34.8 or the center of mass IN THIS EXAMPLE is located 34.8 inches to the left of the center of the right rear tire.
top link ( called 3rd link in race car terms) and axle damper, if used, should be mounted side by side.

one more thing..the rear motion ration , hence wheel rate will impact on proper spring selection..all the power in the world don't mean nothing ifin you can not use it and you need springs and shocks (dampers) to control this action.

 

[Lead Foot]

Ok simple question. Which setup would be overall stronger. The lower control arm mounted on top of the axle tube or below centerline and behind the axle tube? Thats all I am asking. I just want numbers to back it up. I don't need to know my antisquat, antidive, or center roll radius numbers. I have a 3 link calculator for that. I just want to know if the left or right illistration will be stronger and why. Which 2 bolt mounting locations would see the most sheer force?

 

[Lead Foot]

Ranger mike, I only saw your second post. sorry. Its a 4 wheel drive offroading vehicle. Fully locked front and rear (both tires are always under equal power.) This is a FRONT axle, the diff is off to 1 side because if it was in the center it would hit the oil pan... not to mention the transfercase output is also on that side... The upper control arm is on the passenger side because of lack of room due to exhaust and the front driverline on the drivers side. The above question is all I am asking in plain terms. I just want the numbers on the 2 different setups. This is the thing. Some people mount their lower control arm above centerline of the axle tube and sometimes all the way on top to avoid rocks in rock crawling. I just believe the force on the control arms, joints, and mounting bolts would be greatly multiplied in this type of setup. Am I correct?

 

[Ranger Mike]

I am not familiar with the trailing arms being mounted above the axle housing. I can tell you regarding the traditional mounting methods that the geometry or angles of a traditional 3 link system project forward to a common point to form an instant center and thereby behaves like a torque arm. Because of this, be vary careful in the layout of the 3 link point linkage so that this instant center does not have a lot of movement during suspension travel. Having very steep angles of upper and lower arms will create a short instant center causing it to move around. if the suspension travel causes instant center movement the wheels and suspension arms will change angles quite rapidly making for a very unstable feeling for the driver.
I think you will be ok regarding the over tube trail arm mount if you follow the above rule and keep the training arms as long as possible and pretty level to the pavement. the top link can have some angle and can be a lot shorter.

 

[nvn]

Lead Foot: Regarding post 11, OK, could you provide the coordinates mentioned in paragraph 3 of post 8, measured from the axle centerline? And the angles mentioned therein. Also, provide the vertical force N on one wheel.

Note: Instead of giving us the angles, it would be better if you instead give us the coordinates of the upper pin (or end) of each of the three components (strut 1, strut 2, and coil spring). In other words, if you give us the coordinates of each end of each of these three components, then we do not need angles.

 

[nvn]

Lead Foot: Just to give you an idea of what I mean by (x, y) coordinates, measured from the axle centerline ... In your lower, left-hand diagram of post 1, and in your first diagram of post 7, the origin is at the axle centerline and is located at (x, y) = (0, 0) mm. The positive x-axis is horizontal and to the right. The positive y-axis is vertical and upward. In said diagrams, the lower pin of the upper strut (strut 1) might be located at, e.g., (x, y) = (-4, 144) mm. The upper pin of strut 1 might be at, e.g., (880, 283.5) mm. The lower pin of strut 2 might be at, e.g., (68.18, -57.2) mm. The coil spring lower end (at the coil spring centerline) might be at, e.g., (-50, 26) mm. The coil spring upper end (at the coil spring centerline) might be at, e.g., (-55, 491) mm. What are the (x, y) coordinates of your two configurations? See post 14.