Coupled mass problem with orthogonal oscillations

[CAF123]

Homework Statement

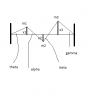
Consider a light elastic string of unstretched length $4a_o$, stretched horizontally on a smooth surface between two fixed points a distance $4a$ apart. ($a > a_o)$. Three particles of mass m are attached so as to divide the string into four equal sections. Number the segments from left to right $i = 1 - 4$. The tension $T_i$ in each segment $i$ is proportional to its extension $(a-a_o)$, with the elastic constant being c>0.

Suppose that the particles are constrained such that they are able to move only perpendicular to the line along which the string is connected. The system as a whole is planar.

1) Write down the eqns of motion for the vertical displacement $x_i$ under the assumption that displacements are small. Keep only linear terms in $x_i/a$. Show that in this approximation, the eqn takes the form $\underline{\ddot{x}} + n^2 A \underline{x} = 0$ and determine $n$ and the matrix $A$.

The Attempt at a Solution

(See diagram for picture)
For mass m1, it is acted upon by T1 and T2. Defining two angles, $\theta, \alpha$ I get $$m_1 \ddot{x_1} = T_1 \sin \theta + T_2 \sin \alpha \Rightarrow m_1 \ddot{x_1} = T_1 \theta + T_2 \alpha$$ in the small angle approx.

To get expressions for the acceleration of the other masses, I defined another two angles $\beta, \gamma$ but the expressions were the same, when I sub in the below for the derived tension force.

Since the system is coupled, if mass m1 moves up then m2 also moves up. So change in length will be $x_i - x_{i-1}$. This gives $T_i X = c[a - a_0 + x_i - x_{i-1}]X, X$ either $\theta, \alpha, \beta, \gamma$. When I sub these in, rearrange I don't get the required form that I need to get to. I did a longitudinal version of this problem , and so I am trying to extrapolate what I did in that problem into this problem. Since we are dealing only with a perpendicular oscillations, the problem is rather similar. I think the $x_i/a$ terms come from expressing sin(X) = xi/a

I can post my working in pen showing detailed drawings etc if required /easier to understand my workings.

Many thanks.

 

[voko]

Since the system is coupled, if mass m1 moves up then m2 also moves up.

You are making the same mistake you did on another coupled problem here recently. Don't assume any simple geometric relationship between the positions of two masses. Treat their coordinates independently. Their only relationship is via the force of tension.

 

[CAF123]

In the horizontal oscillations problem the correct tension force was $T_i = c( a - a_o + x_i - x_{i -1})$. The set up of that problem was exactly the same, except there we had movement of masses longitudinal and not transverse. Is there something i can do with that to apply it to this problem? Do I need to express the tension force in terms of the displacements x1, x2 and x3?

 

[voko]

You just need to find the forces of tension. You started (almost) correctly: the force acting on the first mass is $T_1 \sin \theta + T_2 \sin \alpha$ Now, $T_1 = c (\sqrt {a^2 + x_1^2} - a_0)$, and $\sin \theta = \frac {x_1} {\sqrt {a^2 + x_1^2}}$, so the first term of force is $c (x_1 - \frac {a_0 x_1} {\sqrt {a^2 + x_1^2}}) \approx c(x_1 - \frac {a_0}{a} x_1) = c(1 - \frac {a_0}{a}) x_1$. The second term looks trickier, but observe that the geometry involved is the same, provided we replace $x_1 \rightarrow x_1 - x_2$, so we can fast forward to $c(1 - \frac {a_0}{a}) (x_1 - x_2)$, and the force acting the first mass is $c(1 - \frac {a_0}{a}) (2x_1 - x_2)$.

Now let's go back to the "almost" remark above. Think about the direction of the force and the sign you should assign to $c(1 - \frac {a_0}{a}) (2x_1 - x_2)$.

 

[CAF123]

Hello voko,

You just need to find the forces of tension. You started (almost) correctly: the force acting on the first mass is $T_1 \sin \theta + T_2 \sin \alpha$ Now, $T_1 = c (\sqrt {a^2 + x_1^2} - a_0)$,

Could you explain in a little more detail how you arrived at this expression for $T_1$? I reliase the term you have computed is the hypotenuse of the triangle and so you are saying that this is the extension from the natural length of the string.

EDIT: Also, does the question not say the tension is proportional to a - a0?

The second term looks trickier, but observe that the geometry involved is the same, provided we replace $x_1 \rightarrow x_1 - x_2$

I am not sure I really understand this step.

Now let's go back to the "almost" remark above. Think about the direction of the force and the sign you should assign to $c(1 - \frac {a_0}{a}) (2x_1 - x_2)$.

If I take y as positive down, then $T_1 \sin \theta$ acts downwards and so would be postive.

 

[voko]

Could you explain in a little more detail how you arrived at this expression for $T_1$? I reliase the term you have computed is the hypotenuse of the triangle and so you are saying that this is the extension from the natural length of the string.

Yes, this is the hypotenuse (h) and so is the length of the string between its left-most point and the first mass. Then the force is $c(h - a_0)$.

I am not sure I really understand this step.

The second triangle is very much alike the first triangle. Except its vertical cathetus is $x_1 - x_2$.

If I take y as positive down, then $T_1 \sin \theta$ acts downwards and so would be postive.

What is "y"?

Note it is not important whether "up" is positive or negative. What is important is the direction of $x_1$ and the direction of the force acting on the first mass. Assuming $x_2 = 0$, is it the same direction?

 

[CAF123]

The second triangle is very much alike the first triangle. Except its vertical cathetus is $x_1 - x_2$.

It's still not clear, sorry. What second triangle is alike the first and why did you let $x_1 \rightarrow x_1 - x_2$ in the first place? What does that arrow mean? A mapping?

What is "y"?

Define coordinate system with the positive y direction downwards.

What is important is the direction of $x_1$ and the direction of the force acting on the first mass. Assuming $x_2 = 0$, is it the same direction?

So if m2 stays in place (x2 = 0) and m1 is displaced by x1 vertically (is this what you meant?) then I think the force (T1 sin θ) would still point downwards. If x2 = 0 and x1 = 0 then T1 points leftwards and T2 rightwards.

 

[voko]

Refer to your drawing. The first triangle is the left-most triangle there. The second triangle is the one that follows it, whose vertices are m1 and m2 and the unmarked point under m1 and to the left of m2 (so that the triangle is right).

The arrow means "replace with", just like the text says.

Alternatively, you could consider the case of a string which is stretched to a horizontally, and then its ends are moved vertically so that the vertical distance between them is d. Find out the vertical force of tension in terms of a and d. Then you could translate this to any segment in the original problem, by expressing d via x's.

If x2 = 0, the force is downward if x1 is upward. What does that mean with regard to its sign?

 

[CAF123]

Refer to your drawing. The first triangle is the left-most triangle there. The second triangle is the one that follows it, whose vertices are m1 and m2 and the unmarked point under m1 and to the left of m2 (so that the triangle is right).

The arrow means "replace with", just like the text says.

Alternatively, you could consider the case of a string which is stretched to a horizontally, and then its ends are moved vertically so that the vertical distance between them is d. Find out the vertical force of tension in terms of a and d. Then you could translate this to any segment in the original problem, by expressing d via x's.

If x2 = 0, the force is downward if x1 is upward. What does that mean with regard to its sign?

This means the force is a restoring force so it will have a negative sign. (If upwards is positive) If I define downwards as positive, then the displacement upwards will be negative then the force will be positive. Since the choice does not matter (as you said), take upwards as postive and so the force will be negative.

 

[voko]

This means the force is a restoring force so it will have a negative sign. (If upwards is positive) If I define downwards as positive, then the displacement upwards will be negative then the force will be positive. Since the choice does not matter (as you said), take upwards as postive and so the force will be negative.

Which makes the first equation $m\ddot{x_1} = -c(1 - \frac {a_0} {a})(2x_1 - x_2)$.

 

[CAF123]

Which makes the first equation $m\ddot{x_1} = -c(1 - \frac {a_0} {a})(2x_1 - x_2)$.

Indeed. Before I continue with finding expressions for m2,m3 in terms of x1,x2.. I want to understand your first post well.

So for the first mass, I can write: $$m\ddot{x_1} = -T_1 \sin \theta + T_2 \sin \alpha = -(c(\sqrt{x_1^2 + a^2} - a_o) \cdot \frac{x_1}{\sqrt{x_1^2 + a^2}}) + c(\sqrt{x_2^2 + a^2} -a_o) \cdot \frac{x_2}{\sqrt{x_2^2 + a^2}}. $$Taking the small displacement approx gives in the end, $$c(-x_1 - \frac{a_0}{a}x_1 + x_2 - \frac{a_o}{a}x_2)$$
I don't think it is the same as what you got?

 

[voko]

No it is not. Specifically, the second term is wrong. I advise that you do the "alternative" problem in my post #8. Then apply the solution to the second term.

 

[CAF123]

Alternatively, you could consider the case of a string which is stretched to a horizontally, and then its ends are moved vertically so that the vertical distance between them is d. Find out the vertical force of tension in terms of a and d. Then you could translate this to any segment in the original problem, by expressing d via x's.

So a string has some extension a in the horizontal direction. It then has some vertical extension d. So the distance between the ends is $\sqrt{d^2 + a^2}$. So $T_1 = -c(\sqrt{x_1^2 + a^2} - a_o)$ since $x_1$ is the vertical distance in this case.

For m2, the distance between the ends are x1 + x2. So then $T_2 = c(\sqrt{(x_1 + x_2)^2 + a^2} -a_o)$

 

[voko]

This is correct, but this is not the end. Work out the linear formula for the isolated case, then use it for all the segments.

 

[CAF123]

This is correct, but this is not the end. Work out the linear formula for the isolated case, then use it for all the segments.

Ok, so in general $$T_i = c(\sqrt{(x_j + x_i)^2 + a^2} - a_o)$$, $j = i - 1.$

When I apply this to m2, I get:
m2 moves downwards, so the force points upwards i.e positive in the defined coord. system.
So, $$T_2 \sin \alpha = c(\sqrt{(x_1 + x_2)^2 + a^2} -a_o) \cdot \frac{x_1 + x_2}{\sqrt{(x_1 + x_2)^2 + a^2}}$$
When added to the expression for T1sinθ, I get $$-cx_1 -ca_ox_1/a + c(x_1 + x_2) - \frac{ca_o(x_1 + x_2)}{\sqrt{(x_1+x_2)^2 +a^2}} = + cx_2 - 2ca_ox_1/a - cx_2 a_o/a = -c(2a_ox_1/a - x_2 + x_2 a_o/a)$$ which is close.

 

[voko]

I just noted that you let d = x1 + x2 in #13. This cannot be correct. If x1 = x2, then you get a positive vertical distance, while it should be zero.

Secondly, you did not get the linear formula of force in terms of d. You got Ti (assuming you correct the x1 + x2 issue), but what you need is its vertical component.

 

[CAF123]

I just noted that you let d = x1 + x2 in #13. This cannot be correct. If x1 = x2, then you get a positive vertical distance, while it should be zero.

If m1 goes up by an amount x1 and m2 down by an amount x2, then the distance between them is x1 + x2. Since the string is also stretched in horizontal direction, I sum the squares of these and sqrt (to get the distance between the two ends of that piece of string)?

Secondly, you did not get the linear formula of force in terms of d. You got Ti (assuming you correct the x1 + x2 issue), but what you need is its vertical component.

So, like $$|T_i| = c(\sqrt{(x_i + (?) x_j)^2 + a^2} -a_o) \cdot \frac{(x_i + (?) x_j)}{\sqrt{(x_i + x_j)^2 + a^2}}$$ (I added a question mark because still unsure about this)

 

[voko]

If m1 goes up by an amount x1 and m2 down by an amount x2, then the distance between them is x1 + x2.

You can't use different sign conventions for x1 and x2. If m1 goes up, x1 is positive; if m2 goes down, x2 is negative.

So, like $$|T_i| = c(\sqrt{(x_i + (?) x_j)^2 + a^2} -a_o) \cdot \frac{(x_i + (?) x_j)}{\sqrt{(x_i + x_j)^2 + a^2}}$$ (I added a question mark because still unsure about this)

I suggest you forget about x_i and x_j for a second and solve the simpler problem with vertical separation d - down to expressing the force linearly in d. Then you can substitute x_i and x_j.

 

[CAF123]

You can't use different sign conventions for x1 and x2. If m1 goes up, x1 is positive; if m2 goes down, x2 is negative.

Then I have d = x1 - x2 for m2

I suggest you forget about x_i and x_j for a second and solve the simpler problem with vertical separation d - down to expressing the force linearly in d. Then you can substitute x_i and x_j.

$$|T_i| = c(\sqrt{d^2 + a^2} - a_o) \cdot \left(\frac{d}{\sqrt{d^2 + a^2}}\right)$$
EDIT: Forgot to express down to linear in d...

$$= c(d) - ca_o(d)/a$$

 

[voko]

$$|T_i| = c(\sqrt{d^2 + a^2} - a_o) \cdot \left(\frac{d}{\sqrt{d^2 + a^2}}\right)$$

Linearize this.

 

[CAF123]

Linearize this.

You responded before I had time to put in my edit. See my last post.

 

[voko]

So you got $c(1 - \frac {a_0} {a}) d$, which is correct. Now you just need to find d for each segment and write down the forces in each segment. Minding their signs.

 

[CAF123]

So you got $c(1 - \frac {a_0} {a}) d$, which is correct. Now you just need to find d for each segment and write down the forces in each segment. Minding their signs.

For mass m1: $$m\ddot{x_1} = -c(1 - \frac{a}{a_o})[2x_1 - x_2]$$
For mass m2: $$m\ddot{x_2} = c(1 - \frac{a}{a_o})[x_1 + x_3 - 2x_2]$$
For mass m3: $$m\ddot{x_3} = -c(1 - \frac{a}{a_o})[2x_3 - x_2]$$

 

[voko]

Good.

 

[CAF123]

I have the numerical matrix A and I now have to diagonalise it. I can do this, but just to revise the meaning of diagonilisation from linear algebra: I want to find a matrix P such that $PAP^{-1} = \Lambda,$ where $\Lambda$ is a diagonal matrix.

This is what to means, but what would be the answer to diagonalising A - just finding a P , $P^{-1}$ and $\Lambda$ that makes the above hold?

EDIT: I just noticed this thread was moved to Advanced Physics. I am only in my second year of study. What makes it advanced?

 

[voko]

I have the numerical matrix A and I now have to diagonalise it. I can do this, but just to revise the meaning of diagonilisation from linear algebra: I want to find a matrix P such that $PAP^{-1} = \Lambda,$ where $\Lambda$ is a diagonal matrix.

This is what to means, but what would be the answer to diagonalising A - just finding a P , $P^{-1}$ and $\Lambda$ that makes the above hold?

This usually involves finding eigenvalues and eigenvectors. The technical term is Jordan's normal form.

EDIT: I just noticed this thread was moved to Advanced Physics. I am only in my second year of study. What makes it advanced?

Good question.

 

[CAF123]

This usually involves finding eigenvalues and eigenvectors. The technical term is Jordan's normal form.

I have done it already, but then I have to sketch the normal modes.
My general soln $\underline{x}$ consisted of three terms which all included a cos and sin but each term of the three had a different frequency corresponding to an eigenvalue.

Can you suggest any ways to draw each normal mode? I think what I could do was express each term as a single sin or cos function and then from there read off the amplitude/period. I can see that getting very messy though given my expression for $\underline{x}$.

I could post the expression I got for $\underline{x}$ if more details would help.

 

[voko]

Each normal mode is simply a sinusoidal oscillation at one of the three frequencies you have found multiplied by the corresponding eignenvector. I am not sure what you mean by "drawing", the dimension of the problem makes any drawing challenging to say the least. What are you required to do, exactly?

 

[CAF123]

Each normal mode is simply a sinusoidal oscillation at one of the three frequencies you have found multiplied by the corresponding eignenvector. I am not sure what you mean by "drawing", the dimension of the problem makes any drawing challenging to say the least. What are you required to do, exactly?

The first part of the question I posted in the OP. Part B is as follows:
B) Diagonalise A and determine the general solution for $\underline{x}(t)$. Sketch the form of the three normal modes.

The expression I have for $\underline{x}(t)$ is (if it helps):
$$\beta^1 \underline{P}^1[a\cos\left(\sqrt{\frac{2c}{m}(1-\frac{a_o}{a})}\,\,t \right) + b\sin \left(\sqrt{\frac{2c}{m}(1-\frac{a_o}{a})}\,\,t \right) + \beta^2 \underline{P}^2[a\cos
\left(\sqrt{\frac{c}{m}(1-\frac{a_o}{a})\sqrt{2+\sqrt{2}}}\,\,t \right)+ b\sin \left(\sqrt{\frac{c}{m}(1-\frac{a_o}{a})\sqrt{2+\sqrt{2}}}t\,\, \right) + \beta^3 \underline{P}^3 [a\cos \left(\sqrt{\frac{c}{m}(1-\frac{a_o}{a})\sqrt{2 - \sqrt{2}}}\,\,t \right) + b \sin \left(\sqrt{\frac{c}{m}(1-\frac{a_o}{a})\sqrt{2 - \sqrt{2}}}\,\,t \right)$$

So indeed I do have three normal modes but sketching it ...

 

[voko]

I think you are a bit off with the nested square roots.

Regardless, you should find the normal modes as remarked in #28.

 

[CAF123]

Oh I forgot to actually find the normal modes. I think these modes are defined to be:$$\underline{x^N} = P^{-1} \underline{x}$$. So I should find the inverse of the 3x3 matrix P and multiply it by $\underline{x}$.

I'll probably go to sleep now and do this exercise tomorrow. Many thanks for all your help today.

EDIT: I had a nested sqrt because the freq = $n \sqrt{\lambda_i}$, and the $\lambda_i$ were $2, 2 \pm \sqrt{2}$

 

[voko]

$$\cos \left(\sqrt{\frac{c}{m}(1-\frac{a_o}{a})\sqrt{2+\sqrt{2}}}\,\,t \right)$$

This is definitely wrong. This should be $$\cos \sqrt{\frac{c}{m}(1-\frac{a_o}{a})(2+\sqrt{2})} \,\,t$$ Same for other similar terms where you have nested roots.

I would further suggest that instead of the sin/cos pairs, you could consider using $\sin (\omega t + \alpha)$, the formulae might be more navigable that way.

 

[ehild]

Oh I forgot to actually find the normal modes. I think these modes are defined to be:$$\underline{x^N} = P^{-1} \underline{x}$$. So I should find the inverse of the 3x3 matrix P and multiply it by $\underline{x}$.

You have found the angular frequencies ω. In a normal mode, all masses vibrate with the same frequency but with different amplitudes. So x₁=A₁e^iωt, x₁=A₂e^iωt, x₃=A₃e^iωt. Substitute them back into your equations in post #23, and find the relation between the amplitudes for all the three frequencies.

ehild

 

[CAF123]

You have found the angular frequencies ω. In a normal mode, all masses vibrate with the same frequency but with different amplitudes. So x₁=A₁e^iωt, x₁=A₂e^iωt, x₃=A₃e^iωt. Substitute them back into your equations in post #23, and find the relation between the amplitudes for all the three frequencies.

ehild

I was speaking to some people elsewhere and they said you can get the form of the normal mode by just looking at the eigenvectors in front of each of the terms. How so? Could you explain the physical interpretation of these eigenvectors? (i have my general solution in the earlier posts of this thread)

 

[voko]

See my comment #28.