- #1
Solmyros
- 22
- 0
- TL;DR Summary
- I want to extract the equation describing the coupled mode theory. I am using a book as a reference. I have a question on how he transitioned from one step to another.
edit: Hello everyone! When I posted the question, latex equations that were visible in "preview" do not seem here. So, I upload a pdf version of the question.
We consider zero free charges and currents: ρ=J=0
$$
\mathbf{\nabla} \times \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t} = -\frac{\partial \left( \mu \mathbf{H} + \mathbf{M}\right)}{\partial t} = i \mathbf{\omega} \mathbf{\mu_0} \mathbf{H}, for \: \mathbf{M} = 0
$$
$$
\mathbf{\nabla} \times \mathbf{H} = \frac{\partial \mathbf{D}}{\partial t} = \frac{\partial \mathbf{\left( \epsilon \mathbf{E} + \Delta \mathbf{P} \right)}}{\partial t} = - i \mathbf{\omega} \mathbf{\epsilon} \mathbf{E} - i \mathbf{\omega} \Delta \mathbf{P}
$$
The following two equations describe monochromatic waves of a lossless, unperturbed waveguide.
$$
\mathbf{E_\nu(\mathbf{r})} = \mathbf{\mathcal{E_\nu}}(x, y)exp(i\beta_\nu z)
$$
$$
\mathbf{H_\nu(\mathbf{r})} = \mathbf{\mathcal{H_\nu}}(x, y)exp(i\beta_\nu z)
$$
Generally, we know that normal modes can form a basis. So any optical field at a given frequency, can be expressed in terms of their expansion. And if we have a spatially dependent perturbation to the waveguide, we will have coupling and the amplitude will depend on z, where z is the propagation direction.
I am afraid I will post images here, as my latex code (did it on overleaf) does not show here.

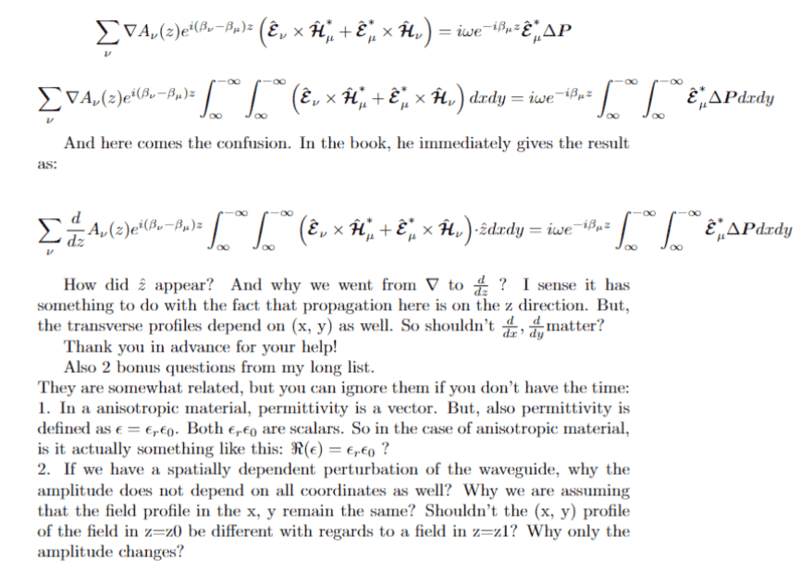
We consider zero free charges and currents: ρ=J=0
$$
\mathbf{\nabla} \times \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t} = -\frac{\partial \left( \mu \mathbf{H} + \mathbf{M}\right)}{\partial t} = i \mathbf{\omega} \mathbf{\mu_0} \mathbf{H}, for \: \mathbf{M} = 0
$$
$$
\mathbf{\nabla} \times \mathbf{H} = \frac{\partial \mathbf{D}}{\partial t} = \frac{\partial \mathbf{\left( \epsilon \mathbf{E} + \Delta \mathbf{P} \right)}}{\partial t} = - i \mathbf{\omega} \mathbf{\epsilon} \mathbf{E} - i \mathbf{\omega} \Delta \mathbf{P}
$$
The following two equations describe monochromatic waves of a lossless, unperturbed waveguide.
$$
\mathbf{E_\nu(\mathbf{r})} = \mathbf{\mathcal{E_\nu}}(x, y)exp(i\beta_\nu z)
$$
$$
\mathbf{H_\nu(\mathbf{r})} = \mathbf{\mathcal{H_\nu}}(x, y)exp(i\beta_\nu z)
$$
Generally, we know that normal modes can form a basis. So any optical field at a given frequency, can be expressed in terms of their expansion. And if we have a spatially dependent perturbation to the waveguide, we will have coupling and the amplitude will depend on z, where z is the propagation direction.
I am afraid I will post images here, as my latex code (did it on overleaf) does not show here.
Attachments
Last edited by a moderator: