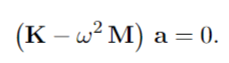Coupled oscillator question

[ChiralSuperfields]

Homework Statement

Please see below

Relevant Equations

$(\vec K - \omega^2\vec M)\vec a = \vec 0$

The problem and solution is,

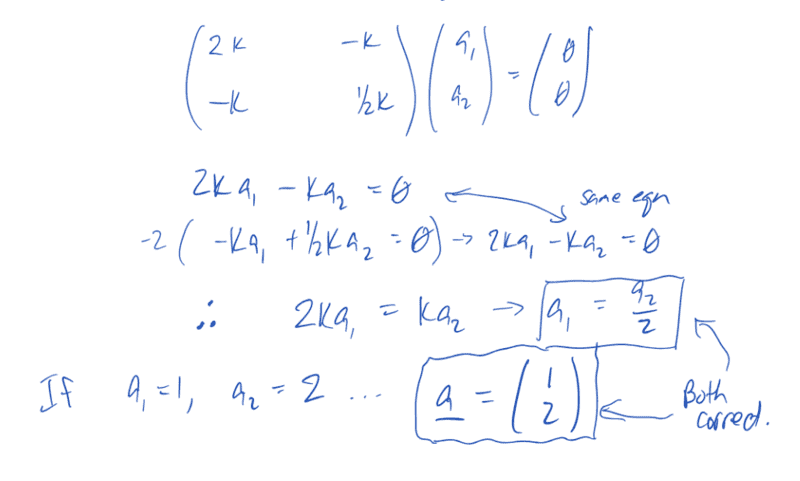
However, I am confused how they get $\vec a = (1, 2)$ (I convert from column vector to coordinate form of vector). I got $\vec a = (a_1, a_2) = (a_1, 2a_1) = a_1(1, 2)$ however, why did they eliminate the constant $a_1$?

Thanks for any help!

 

[Henryk]

This is a classic coupled oscillators problem. The solution involves finding the eigenvalues of the matrix, that is the values of $\omega$ which will make the determinant of the matrix equal to zero. That part is already done for you and you are given one value of normal frequency equal to $\omega = \sqrt{\frac k {2m}}$ (the other normal frequency is $\omega = \sqrt{\frac {3k} {2m}}$).
Your job is to find the eigenvector that correspond to the normal frequency given. $a_1$ and $a2$ are amplitudes of, respectively, the first and the second mass and what really matters is not the absolute value of the amplitudes but their relative values. Your answer is correct, the amplitude of the second mass is twice the amplitude of the first mass and, they are moving in the same direction. However, the actual values of the amplitudes can be anything, 0 cm, 10 cm, etc., $a_1$ is not a constant, can be anything.
Incidently, if you were to use the other frequency, you would have found that the masses oscillate out of phase yet, the amplitude of the second mass is also double the first one.

 

[kuruman]

However, I am confused how they get $\vec a = (1, 2)$ (I convert from column vector to coordinate form of vector). I got $\vec a = (a_1, a_2) = (a_1, 2a_1) = a_1(1, 2)$ however, why did they eliminate the constant $a_1$?

It's the ratio $a_1/a_2$ that counts. The normal modes are conventionally written as normalized column vectors. In this case, one would write $$\mathbf a =\frac{1}{\sqrt{5}}
\begin{pmatrix}1 \\2\end{pmatrix}.$$