Coupled oscillators -- period of normal modes

[happyparticle]

Homework Statement

I have to determine the periods of the normal modes.

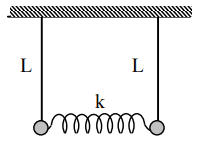
I have 2 mass $m_1 = m_2$, l = 1.2m and if I hold vertically one of the mass the period of the other mass is 1.5s.

Relevant Equations

F = ma

$m\ddot x = -\frac{mgx_1}{l} -k(x_1 - x_2)$
$m\ddot x_2 = -\frac{mgx_2}{l} +k(x_1 - x_2)$

Hi,

I know there's are 2 normal modes because the system has 2 mass. I did the Newton's law for both mass.

$m\ddot x_1 = -\frac{mgx_1}{l} -k(x_1 - x_2)$ (1)
$m\ddot x_2 = -\frac{mgx_2}{l} +k(x_1 - x_2)$ (2)

In the pendulum mode $x_1 = x_2$ and in the breathing mode $x_1 = -x_2$

I get the pendulum and breathing mode by adding equation 1 and 2 and subtracting 1 and 2 then I replace $x_1-x_2$ by q2 and $x_1+x_2$ by q1.
Finally I have $\omega_p = \sqrt{\frac{g}{l}}$ and $\omega_b = \sqrt{\frac{g}{l} + \frac{2k}{m}}$
It's quite easy to get the period for $\omega_p$. However, I'm not sure how to find the period for $\omega_b$, since I don't have k and m.

 

[haruspex]

You will need to supply a diagram or a full description of the physical arrangement. In particular, I am confused regarding whether these x displacements are horizontal or vertical.

 

[happyparticle]

You will need to supply a diagram or a full description of the physical arrangement. In particular, I am confused regarding whether these x displacements are horizontal or vertical.

My bad, sorry. I uploaded an image.

 

[haruspex]

My bad, sorry. I uploaded an image.

Doesn't this tell you k/m?
"if I hold vertically one of the mass the period of the other mass is 1.5s."

 

[happyparticle]

Doesn't this tell you k/m?
"if I hold vertically one of the mass the period of the other mass is 1.5s."

I need to find the period for the normal modes. I don't see the link between 1.5s and the normal modes.

 

[haruspex]

I need to find the period for the normal modes. I don't see the link between 1.5s and the normal modes.

You wrote that what was blocking you was that you did not know k/m.
What wouid the period be if you suspended one of the masses from the other and let it oscillate vertically?

 

[happyparticle]

I see...

Can I plug $\frac{1.5}{2\pi}$ to find $\omega_b$?

It seems too easy.

 

[haruspex]

I see...

Can I plug $\frac{1.5}{2\pi}$ to find $\omega_b$?

It seems too easy.

not quite that simple... it tells you k/m. Your equation for $\omega_b$ has another term

 

[happyparticle]

$\omega_b = \sqrt{\frac{g}{l} + \frac{2k}{m}}$
$g = 9.8$ and $l = 1.2$

$\omega_b = \sqrt{8.2 + 2(\frac{1.5}{2pi})}$

Is it correct?

 

[haruspex]

$\omega_b = \sqrt{\frac{g}{l} + \frac{2k}{m}}$
$g = 9.8$ and $l = 1.2$

$\omega_b = \sqrt{8.2 + 2(\frac{1.5}{2pi})}$

Is it correct?

Doesn’t look right to me.
What is the expression for the period of a mass on a spring?

 

[happyparticle]

Right, I made a mistake.

$\omega_b = \sqrt{8.2 +2(\frac{2\pi}{1.5})^2}$

 

[haruspex]

Right, I made a mistake.

$\omega_b = \sqrt{8.2 +2(\frac{2\pi}{1.5})^2}$

Right.