PainterGuy
- 938
- 73
- Homework Statement
- Having problem getting the correct answer using Cramer's rule.
- Relevant Equations
- Please check my work in the posting.
Hi,
I did the first degree curve fitting in MATLAB. Please see below which also shows the output for each code line.
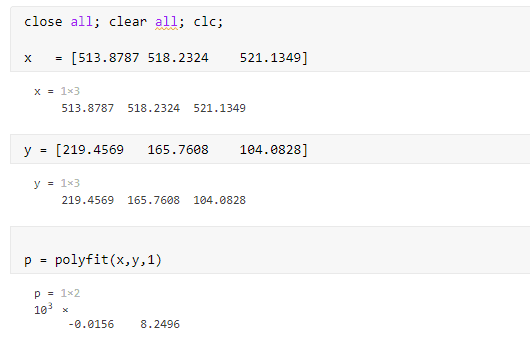 But I wasn't able to get the same answer using Cramer's rule method presented below. I'm sure MATLAB answer is correct so where am I going wrong with the Cramer's rule method. Could you please guide me?
But I wasn't able to get the same answer using Cramer's rule method presented below. I'm sure MATLAB answer is correct so where am I going wrong with the Cramer's rule method. Could you please guide me?
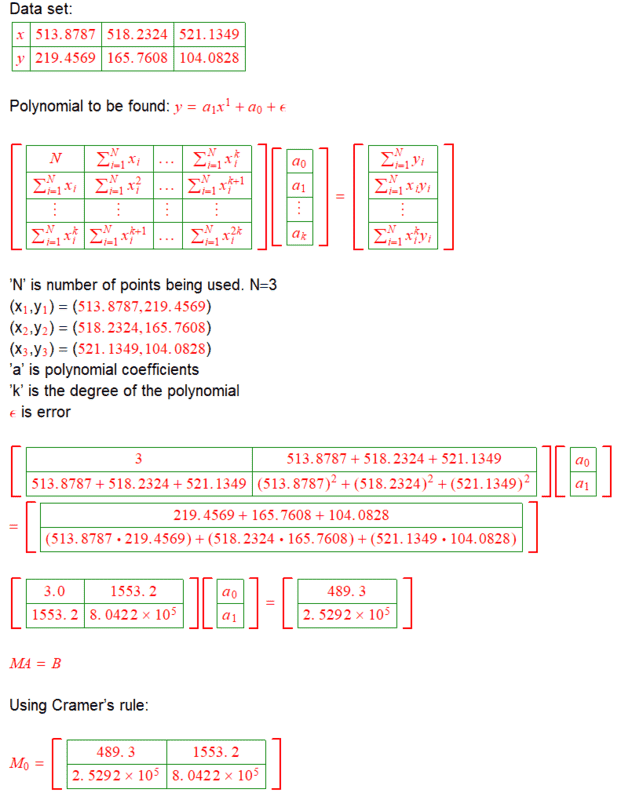
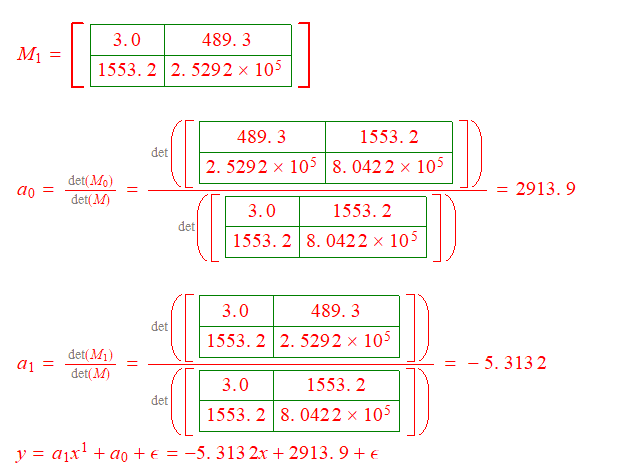
I did the first degree curve fitting in MATLAB. Please see below which also shows the output for each code line.