- #1
TimeRip496
- 254
- 5
Is it possible to create a concentric circles whereby all the objects on it have equal distance from each other?
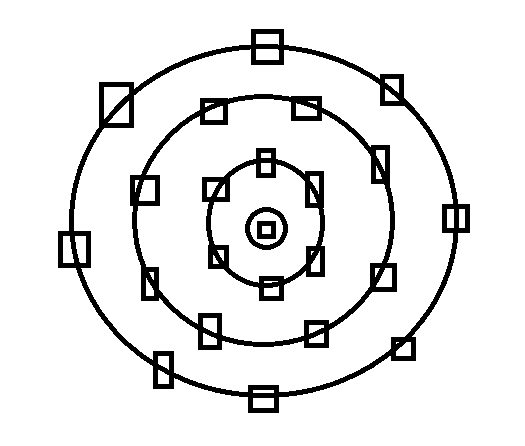
where the squares/rectangles are object and are equal distance from each other regardless on what circle they are on.
Thanks!
where the squares/rectangles are object and are equal distance from each other regardless on what circle they are on.
Thanks!