Kekkuli
- 9
- 2
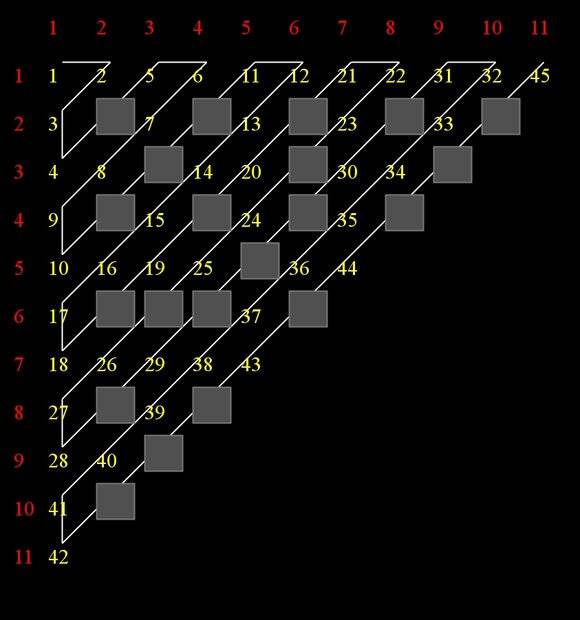
On the one hand, Cantor showed that not all real numbers can be enumerated, while on the other hand he showed that rational numbers can. Cantor demonstrated this with a grid. In the picture below, a natural number (yellow) is assigned to each rational number in order, but since the natural number is also a rational number, a fractional number that has not yet been listed has been constructed in each listing step. In the picture below, the largest number among the rational numbers is 11/1=11, while the largest natural number is already 45, it follows that all fractions can never be listed. Enumeration always produces only more numbers that have not yet been enumerated.