Cross product of complex vectors

[s_guo82]

Would you pls help me with the following vector product? I got no idea how the author derived the second equation from the first one. My derivation result is always including the imaginary unit i for the second term in the second equation on the right hand side. Specifically, how to verify that the cross product of the complex vector and its conjugate is equal to the cross product of the real part of the complex vector and the its imaginary part? ~ denotes a complex variable.

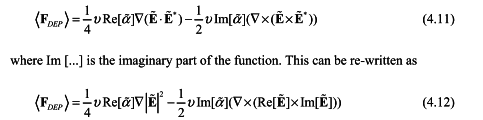
Thank you in advance

 

[Petr Mugver]

Looks like a -2i factor is missing in the second term of the second equation. You get this as well?

 

[s_guo82]

Yes, I got the same thing. I doubt there should be a "i" for the second term on the right hand side of the second equation. However, all the author's simulation is based on the second equation. I also tried to expand the first equation and simulated it, but it did not give a result that makes sense. However, with the second equation, the simulation result seems to make sense. I asked this question because I am neither a maths student nor physics and I am not confident that the renowned author can make mistakes for such an important expression. He used this equation all the way in his book.

This is from the book "AC electrokinetics: Colloids and nanoparticles" by Morgan and Green.

Any other thoughts, guys?